■ 목표
- 3차식으로 나눈 나머지 구하기
- 문제구조 살펴보기

<참고> 이어지는 내용입니다.
나머지정리1 [1차식/2차식으로 나눈 나머지]
■ 목표 - 나머지정리 이해하기 - 1차식/2차식으로 나눈 나머지 구하기 - 나머지정리 문제구조 살펴보기 나머지정리 개요 나머지를 가장 효율적으로 구하는 방법은 수치대입법을 활용하는 것이
indv-wrappedmath.tistory.com
C-1. 3차식으로 나눈 나머지(인수분해됨)
이번에는 어떤 식을 (3차식)으로 나눈 경우입니다.
(3차식)이라 복잡하긴 해도 만약
(1차식)(1차식)(1차식)으로 인수분해가 된다면
방법 자체는 간단합니다.
■ 3차식으로 나눈 나머지 구하기1
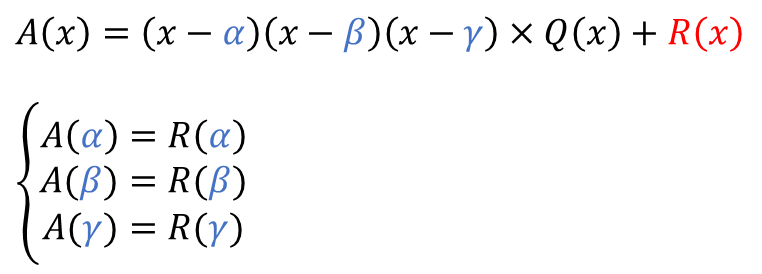
① $R(x)$ 는 3차식보다 작은 2차식입니다.
② $R(x)$$=ax^2+bx+c$ 라고 할 수 있습니다.
③ $x=α$, $x=β$, $x=γ$ 를 대입합니다.
하지만, 미정계수가 $a, b, c$ 3개인 이상
연립방정식을 푸는데 꽤나 고생을 해야겠죠.
예로 문제를 하나 풀어보겠습니다.
■ 예제
$A(x)$ 를 $x$ 로 나눈 나머지는 $4$, $x-1$ 로 나눈 나머지는 $1$, $x-2$ 로 나눈 나머지는 $2$ 이다.
이때, $A(x)$ 를 $x(x-1)(x-2)$ 로 나눈 나머지를 구하시오.
(풀이)
우선, 삼차식으로 나눈 나머지이므로
$R(x)=ax^2+bx+c$ 라고 할 수 있습니다.
일차식으로 나눈 나머지들을 통해
$A(0)=4$, $A(1)=1$, $A(2)=2$ 임을 알 수 있습니다.
$A(x)=x(x-1)(x-2)Q(x)+R(x)$ 이므로,
$x=0, 1, 2$ 를 대입합니다.
$4=R(0)=c$
$1=R(1)=a+b+c$
$2=R(2)=4a+2b+c$
연립해서 풀어주면
$a=2$, $b=-5$, $c=4$
$R(x)=2x^2-5x+4$ 입니다.
C-2. 3차식으로 나눈 나머지(인수분해 안됨)★
이번엔 (3차식)이 인수분해가 되긴 하는데
(1차식)(2차식)으로 인수분해가 된다면 어떨까요?
많은 학생들이 가장 어려워하는 유형이죠.
천천히 살펴볼게요.
$A(x)$ 를 $(x-α)B(x)$ 로 나눈 식입니다.

우선, $(x-α)$ 로 나눈 나머지를 이용하는 방법은
그냥 $x=α$ 를 대입하는 것(수치대입법)입니다.
$A(α)=R(α)$ 라는 결과를 얻을 수 있죠.
하지만, $B(x)$ 는 어떻게 이용할까요?
대입해서 $B(x)=0$ 이 되는 $x$ 가 없다면
수치대입법 활용이 어렵습니다.
그래서 위 식에서
$B(x)$ 로 나누었을 때의
"몫과 나머지가 어떻게 변형"되는지 살펴볼게요.
<참고>
몫과 나머지의 변형
■ 목표 - B가 변할 때, Q와 R의 변화 알아보기 - B(x)가 변할 때, Q(x)와 R(x)의 변화 알아보기 나눗셈에서 몫과 나머지 변형 나눗셈의 목적은 몫(Q)과 나머지(R)를 구하는 것이고. 당연히 "뭘로 나누냐"
indv-wrappedmath.tistory.com

우선, $(x-α)$ 는 $Q(x)$ 에 곱해지면서
새로운 몫이 됩니다.
그리고 $B(x)$ 가 (2차식)이고, $R(x)$ 도 (2차식)이기 때문에
"$B(x)$ 는 $R(x)$ 를 나눌 수 있습니다!"
이렇게 말이죠.

(2차식)÷(2차식)을 하면
몫은 상수이고, 나머지는 (1차식)입니다.
이를 이용해서
$B(x)$ 로 나눈 나머지를 정리해볼게요.

잘 살펴보면
$A(x)$ 를 $B(x)$ 로 나눈 나머지와
$R(x)$ 를 $B(x)$ 로 나눈 나머지는
같습니다.
이 중요한 내용을 이해하면
생각보다 훨씬 편하게
$R(x)$ 를 구할 수 있습니다.
■ 3차식으로 나눈 나머지 구하기2
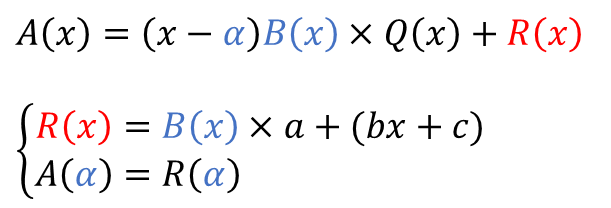
① $R(x)$ 는 3차식보다 작은 2차식입니다.
② $B(x)$ 를 이용하여, $R(x)$$=a$$B(x)$$+bx+c$ 라고 할 수 있습니다.
③ $x=α$ 를 대입합니다.
예로 문제를 하나 풀어보겠습니다.
■ 예제
$A(x)$ 를 $x^2+x+1$ 로 나눈 나머지는 $2x-1$, $x-1$ 로 나눈 나머지는 $4$ 이다.
이때, $A(x)$ 를 $(x-1)(x^2+x+1)$ 로 나눈 나머지를 구하시오.
(풀이)
$R(x)$ 는 이차식입니다.
$A(x)$ 를 $x^2+x+1$ 로 나눈 나머지는 $2x-1$ 이다.
즉, $R(x)$ 를 $x^2+x+1$ 로 나눈 나머지는 $2x-1$ 이다.
이를 통해, $R(x)=a(x^2+x+1)+2x-1$ 이라고 놓을 수 있습니다.
$x-1$ 로 나눈 나머지가 $4$ 이므로,
$R(1)=3a+1=4$
즉, $a=1$ 입니다.
$R(x)=x^2+3x$
마무리
여기까지! 어땠나요?
나름 수학(상)에서 많은 학생들이 좌절시킨
첫 번째 보스 역할을 담당하고 있는 유형입니다.
몇 가지 포인트만 잘 이해하면 충분히 할 수 있는 유형이니
잘 연습하면 될 거예요.
'공통수학1 [고1] > 2. 항등식과 나머지정리' 카테고리의 다른 글
| 인수정리 (0) | 2022.11.14 |
|---|---|
| 몫과 나머지의 변형 (0) | 2022.11.08 |
| 나머지정리1 [1차식/2차식으로 나눈 나머지] (0) | 2022.11.07 |
| 나눗셈에 대한 항등식 (0) | 2022.11.06 |
| 항등식의 풀이 - B. 수치대입법 (0) | 2022.10.10 |





댓글