나눗셈에 대한 항등식

■ 목표

- 나눗셈에 대한 항등식 이해하기

- 나눗셈에 대한 항등식을 푸는 방법

 

 

 

 

나눗셈에 대한 항등식

 

결론부터 얘기하면 이겁니다.

"나눗셈에 대한 등식은 항등식이다!"

 

 

나눗셈에 대한 등식은

나누는 과정을 식으로 쓴 것입니다.

 

 

"식  $A(x)$ 를 식  $B(x)$ 로 나눈다."

그 과정을 등식으로 쓰면 이렇게 되죠.

 

 

 

 

등식에는 다시 방정식과 항등식이 있는데요

그렇다면 이 등식은 둘 중 뭘까요?

 

 

이 식은 그냥  "나눗셈 과정을 그대로 쓴 식" 이기 때문에,

오른쪽을 계산하면 왼쪽 식이 나오죠.

 

 

즉, 등호(=)를 기준으로 왼쪽과 오른쪽의 두 식은

완전히 동일합니다.

그래서, 항등식입니다.

 

 

이 의미를 담아  "나눗셈에 대한 등식" 대신

"나눗셈에 대한 항등식" 이라고 부르기로 합니다.

 

 

 

나눗셈에 대한 항등식 풀이

 

 

항등식의 풀이라면

$x$ 를 구하는 게 목적이 아닙니다.

어떤 식의 미정계수를 구하는 거죠.

 

 

바로  $Q(x)$ 와  $R(x)$ 입니다.

$A(x)$ 와  $B(x)$ 를 이용해서,  $Q(x)$ 와  $R(x)$ 를 구하는 것이 목적입니다.

 

 

한번 예를 들어 생각해보죠.

 

---

■ 예시

$2x^3-x^2+4x-10$ 을  $x-2$ 로 나누었습니다.

 

 

물론 나눗셈을 배웠으니 직접 나누어도 되지만,

이번에는 항등식임을 이용해서 구해볼 겁니다.

 

 

■ 나눗셈에 대한 항등식 풀이

① $Q(x)$ 와  $R(x)$ 를 식으로 세우기

② 미정계수법 - 미정계수 구하기

 

​

① $Q(x)$ 와  $R(x)$ 를 식으로 세우기

우선은 차수를 알아야 식을 세울 수 있습니다.

 

 

왼쪽의 식이 3차식이기 때문에, 

1차식인  $(x-2)$ 에 곱해진 $Q(x)$ 는

2차식이어야 합니다.

따라서,  $Q(x)=ax^2+bx+c$ 라고 놓을 수 있습니다.

 

 

$R(x)$ 는  1차식인 $(x-2)$ 로

나눌 수 있는 만큼 전부 나누고 남은 나머지

즉, 상수입니다.

따라서,  $R(x)=d$ 라고 놓을 수 있습니다.

 

 

<참고> 다항식의 나눗셈

다항식의 나눗셈

 

 

이렇게 식을 세워보면

 

 

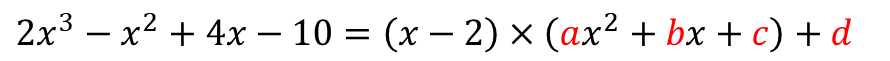
이제 구해야 할 미정계수들이 보입니다.

 

---

 

② 미정계수법

미정계수인  $a, b, c, d$ 를 구하는 방법입니다.

전부 전개해서 비교하는 계수비교법과

특정 수치를 대입하는 수치대입법이 있었죠.

 

 

근데 여기서 몫의 계수인  $a, b, c$ 를 구하기 위해서는

꽤 복잡한 과정이 필요합니다.

 

 

3차, 2차, 1차항을 전개해서 비교하거나

수치를 대입하더라도 최소 3번은 해야 하죠.

 

 

하지만, 나머지인  $d$ 는 굉장히 효율적으로 구할 수 있습니다.

바로  $x$ 에  $2$ 를 대입하는 것이죠!

$16-4+8-10=d$

즉,  $R(x)=10$ 입니다.

 

 

<참고> 수치대입법

항등식의 풀이 - B. 수치대입법

 

 

우리는 이 혁신적인 방법을 이용하기 위해

몫은 굳이 구하지 않고,

나머지를 구하는 것에만 집중해보기로 합니다.

 

 

"수치대입법을 이용해서 나머지를 구한다."

이를 나머지정리라고 합니다.

 

 

 

마무리

 

여기까지!

다음엔 나머지정리에 대해 더 자세히 알아볼게요!