■ 목표
- 다항식의 나눗셈에 대한 등식 이해하기
- 다항식의 나눗셈 원리 이해하기

다항식의 나눗셈에 대한 등식
식을 식으로 나누면 어떻게 될까요?
"$A(x)$ 라는 식을 $B(x)$ 라는 식으로 나눈다."
나눗셈에 대한 등식으로 써보면 이렇게 됩니다.

이제 우리가 찾아야하는 몫도 나머지도 모두
$x$ 에 대한 식입니다.
어떤 식을 찾아내고 싶을 때,
가장 먼저 할 수 있는 일은 바로 몇 차식인지를 알아내는 것이죠.
즉, 차수를 구하는 것이 가장 중요합니다.
■ 몫과 나머지의 차수
① $Q(x)$의 차수
$A(x)$의 차수 = $B(x)$의 차수 + $Q(x)$의 차수
② $R(x)$의 차수
$R(x)$의 차수 $\leq$ $B(x)$의 차수
$A(x)$ 는 $B(x)$ 와 $Q(x)$ 의 곱입니다.
$x^5$ 을 만드려면, $x^2$ 에 $x^3$ 을 곱해야하죠.
즉, (5차식)을 (2차식)으로 나누었다면, 몫은 (3차식)이 됩니다.
나머지인 $R(x)$ 는 $B(x)$ 로 최대한 나누고 남은 식입니다.
그래서 무조건 $B(x)$ 보다는 차수가 낮습니다.
즉, (5차식)을 (2차식)으로 나누었다면, 나머지는 (1차식)보다 작다는 뜻이죠.
다항식의 나눗셈
이제 실전 나눗셈을 해볼게요.
열심히 전개했던 식 중 하나를 생각해보죠.

이 식의 순서를 바꿔보면 나눗셈에 대한 등식이 됩니다.


즉, " $x^2+5x+6$ 이라는 식을 $(x+2)$ 로 나누었을 때, 몫은 $(x+3)$ 이고 나머지는 없다."
이렇게 볼 수 있겠죠.
여기서 만약 몫이 숨겨져 있었다면 어떤 방법으로 찾아야 할까요?
■ 예시1

① $Q(x)$ 의 차수
(2차식)=(1차식)$\times$(1차식)
즉, $Q(x)$ 는 $x$ 에 대한 1차식입니다.
② $Q(x)$ 의 항 찾기
왼쪽의 최고차항인 $x^2$ 을 만들기 위해서는
$Q(x)$의 최고차항이 $x$ 여야 합니다.
즉, $Q(x)=(x+a)$ 입니다.
그 이후는 계산을 해보면서 맞춰갑니다.

서로 식을 비교해보면서 $a=3$
즉, $Q(x)=(x+3)$ 임을 찾아낼 수 있습니다.
■ 예시2
그럼 이번엔 같은 식을 $(x+1)$ 로 나누어보면 어떻게 될까요?
일단 나눗셈에 대한 등식으로 표현해봅니다.
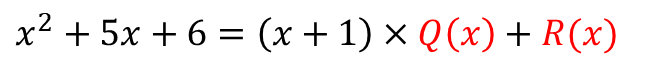
같은 방법으로 $Q(x)$ 부터 찾아볼까요?
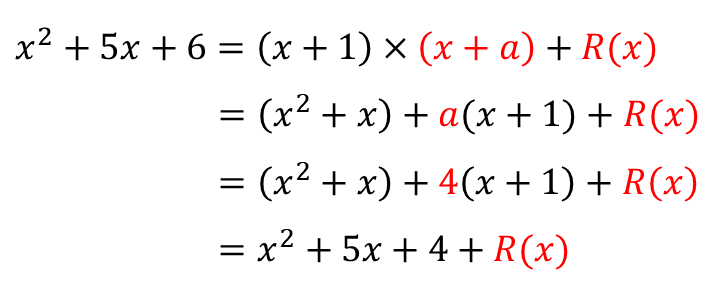
몫 $Q(x)$ 가 $(x+4)$ 라는 걸 찾아내고 나면,
자연스럽게 나머지 $R(x)$ 가 $2$ 라는 것도 알 수 있죠.
즉, 다항식의 나눗셈의 원리는
계속 왼쪽 식과 오른쪽 식을 비교해가며 맞춰가는 것입니다.
마무리
여기까지!
왠지 계산보다는 추리하는 것처럼 느껴지죠?
다음엔 좀 더 간결한 방법인 세로셈법으로 나눠볼게요.
'공통수학1 [고1] > 1. 다항식의 연산' 카테고리의 다른 글
| 조립제법 유도과정 (0) | 2022.10.03 |
|---|---|
| 세로셈법 (0) | 2022.09.30 |
| 나눗셈에 대한 등식 (2) | 2022.09.23 |
| 파스칼의 삼각형 [심화] (0) | 2022.09.23 |
| 곱셈공식의 변형 (1) | 2022.09.23 |





댓글