파스칼의 삼각형 [심화]

■ 목표

- 이항계수 알아보기

- 파스칼의 삼각형 알아보기

- A. 시어핀스키 삼각형과의 관계

- B. 이항계수와의 관계 [고1 수학(상)]

- C. 조합과의 관계 [고1 수학(하)]

- D. 수열과의 관계 [고2 수학1]

 

 

 

 

 

이항계수

 

먼저, 이항계수의 뜻을 알아볼게요.

이항이란 "항이 2개"임을 뜻합니다.

즉, 이항식은  $(a+b)$, $(x+y)$ 같은 식을 말하죠.

 

 

이항식을 여러 번 곱해서 전개해보면

각 항들의 계수들이 생길 텐데요.

이를 줄여서, 이항계수라고합니다.

 

---

 

$(a+b)$ 를 여러 번 곱해서 전개한 뒤

$a$ 를 기준으로 내림차순 정리를 해보면

다음과 같습니다.

 

 

$(a+b)^1=a+b$

$(a+b)^2=a^2+2ab+b^2$

$(a+b)^3=a^3+3a^2b+3ab^2+b^3$

 

 

여기서 계수에만 집중해보면

 

 

$1$, $1$

$1$, $2$, $1$

$1$, $3$, $3$, $1$ 이죠.

 

---

 

이 이항계수들을 굉장히 많이 찾아낸 다음

삼각형 모양으로 배치한 것을

파스칼의 삼각형이라고 합니다.

 

 

이 삼각형을 한번 만들어보고

어떤 규칙들이 숨어있는지 살펴보고자 합니다.

 

 

 

파스칼의 삼각형 만들기

 

이것이 파스칼의 삼각형입니다.

 

파스칼의 삼각형

 

보기 좋도록 제일 윗 칸에도 1을 썼죠.

8줄까지 썼지만

물론 끝도 없이 계속 쓸 수 있습니다.

방법은 다음의 두 가지를 따라 하면 됩니다.

 

 

① 모든 줄의 양쪽 끝은 1이다.

 

 

② 윗줄의 이웃한 두 수를 더하면 바로 아래의 수가 나온다.

 

 

 

A. 시어핀스키 삼각형과의 관계

 

폴란드 수학자인 시어핀스키(Wacław Sierpiński)의 이름을 딴 삼각형으로

닮음 혹은 수열 문제에서 가끔 등장하는 도형입니다.

 

 

시어핀스키 삼각형

 

 

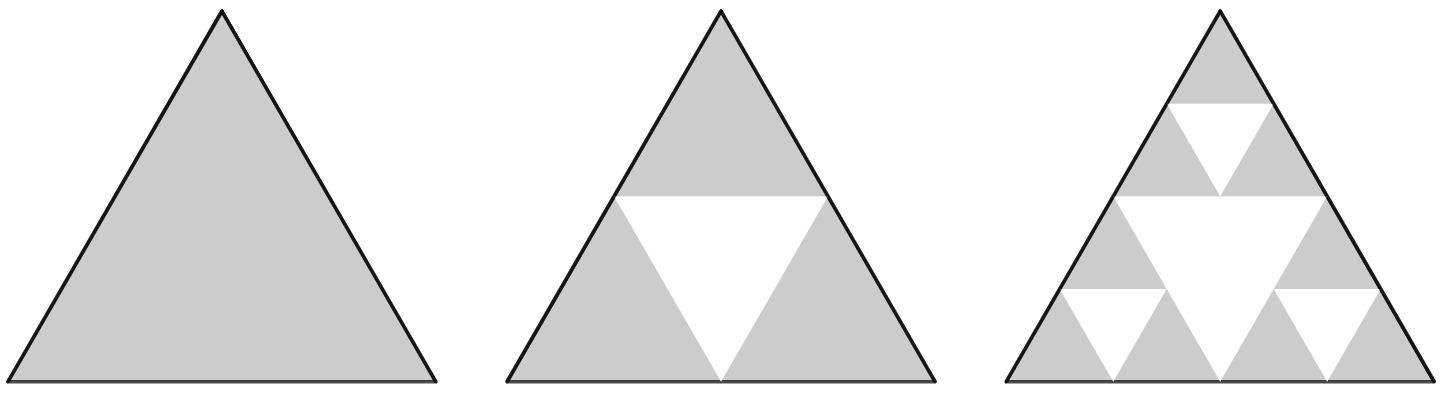
이런 식으로 각 변의 중점을 이어서 만든 삼각형을

잘라내는 것을 무한히 반복하는

일종의 프랙탈 도형입니다.

 

 

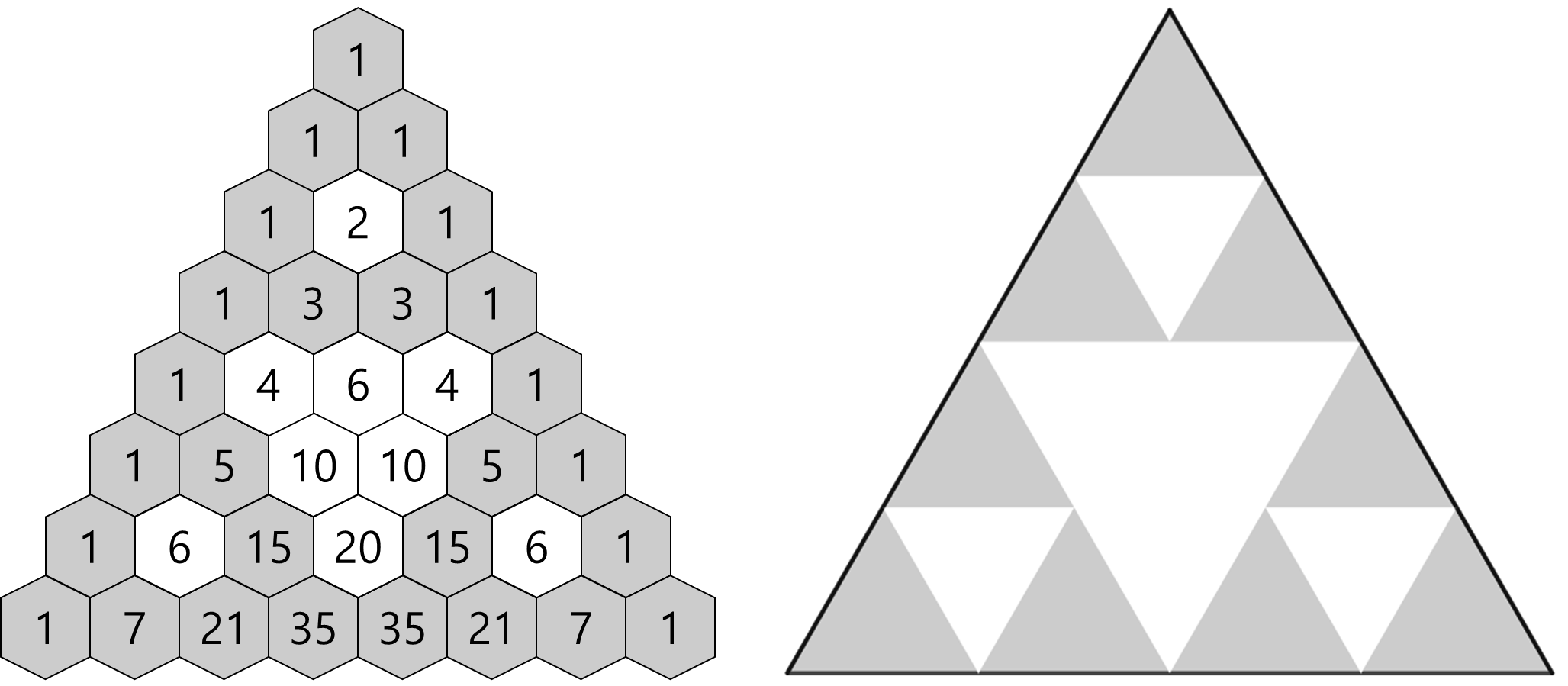
신기하게도 파스칼의 삼각형에서

홀수와 짝수를 구분 지어 다른 색을 칠해보면

같은 모양이 발견됩니다. 

 

 

 

 

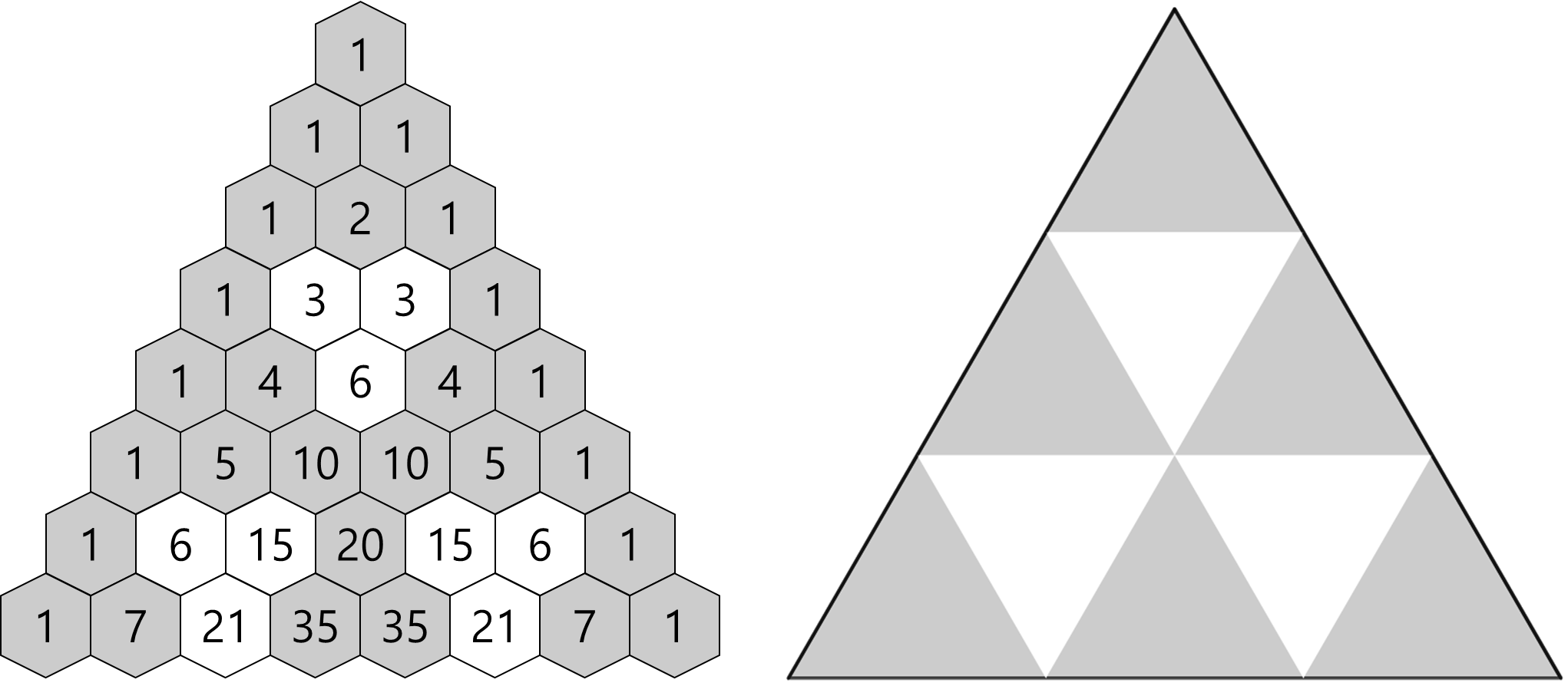
이번엔 3의 배수만 색깔을 지워보면

삼중점을 이어서 만든 삼각형을 잘라낸 도형과

같은 모양이 됩니다.

 

 

 

 

이처럼 특정 배수들을 다른 색으로 칠해보면

파스칼의 삼각형은 모두 프랙탈 도형이 됩니다.

신기하죠?

 

 

 

B. 이항계수와의 관계 [고1-수학(상)]

 

① 삼각형의 각 줄은  $(a+b)^n$ 의 거듭제곱에서 각 항의 계수를 나타낸다.

 

 

 

 

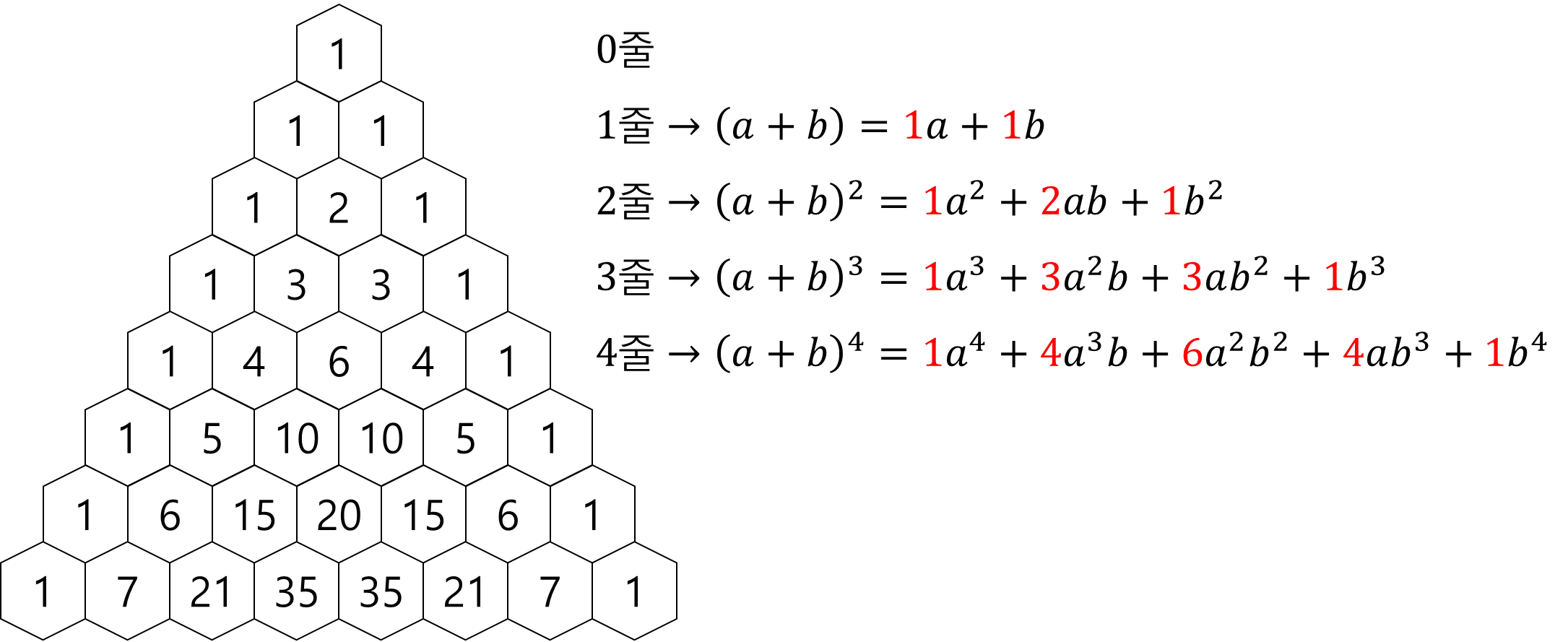
② 각 줄의 합은  $2^n$ 이다.

$a=1$,  $b=1$ 을 대입해보면 알 수 있습니다.

$(a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4$

$2^4=1+4+6+4+1$

즉, 4번째 줄의 합은  $2^4$ 입니다.

 

 

③ 각 줄의 교대(+,-)합은  $0$이다.

$a=1$,  $b=-1$ 을 대입해보면 알 수 있습니다.

$(a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4$

$0=1-4+6-4+1$

 

 

다른 말로, 각 줄에서

짝수번째 수들의 합과 홀수번째 수들의 합은 같습니다.

 

 

 

C. 조합과의 관계 [고1-수학(하)]

 

$(a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4$ 에서 보면

$a^3b$ 의 계수는 $4$ 입니다.

 

 

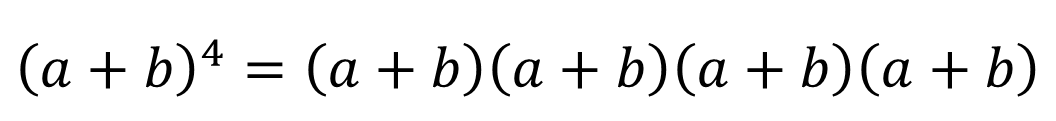
4개의 이항식  $(a+b)$ 에서

$a$ 를 3개,  $b$ 를 1개만 뽑는 경우의 수죠.

이를 조합,  $_4C_3$ 이라고 표현합니다.

 

 

순서대로

$a$,  $a$,  $a$,  $b$

$a$,  $a$,  $b$,  $a$

$a$,  $b$,  $a$,  $a$

$b$,  $a$,  $a$,  $a$

 

 

이렇게 4가지 방법이 있으므로,

$_4C_3=4$ 입니다.

 

 

이처럼 이항계수는 모두

조합으로 표현할 수 있다는 걸 알 수 있습니다.

그래서 파스칼의 삼각형도 다음과 같이 표현할 수 있죠.

 

 

 

 

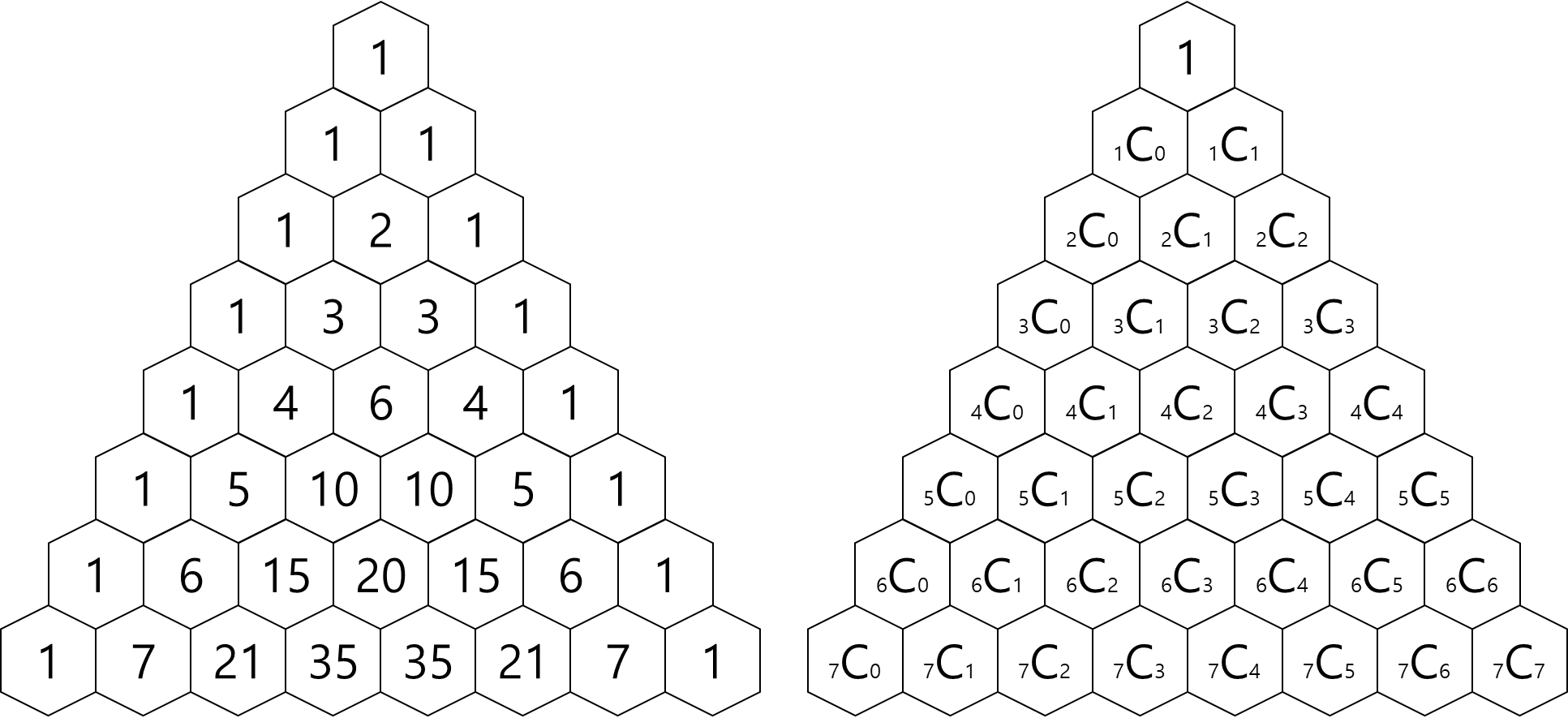
여기서 알 수 있는 

조합의 중요한 성질들을 살펴볼게요.

 

 

①  $_nC_0=1$,  $_nC_n=1$

$n$개 중  $0$개를 뽑는 경우와

$n$개중  $n$개를 뽑는 경우의 수는  $1$이다.

파스칼의 삼각형에서 양 쪽 끝이  $1$ 이라는 것을 보면

바로 알 수 있습니다.

 

 

②  $_nC_r =$ $_{n}C_{n-r}$

예를 들어,  $_4C_3 =$ $_4C_1$

즉,  $4$개 중  $3$개를 뽑는 경우

$4$개 중  $1$개를 뽑는 경우는 같습니다.

파스칼의 삼각형이 좌우대칭임을 이용하면

바로 알 수 있습니다.

 

 

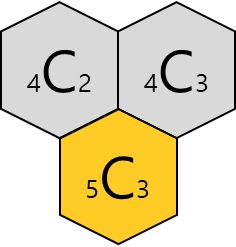
③  $_nC_r =$ $_{n-1}C_{r-1}+$ $_{n-1}C_{r}$ 

예를 들어,  $_5C_3 =$ $_4C_2+$ $_4C_3$ 

$4$개 중  $2$개를 뽑는 경우와

$4$개 중  $3$개를 뽑는 경우를 더하면

$5$개 중  $3$개를 뽑는 경우와 같습니다.

이는 파스칼의 삼각형을 만드는 원리와 같죠.

 

 

 

 

 

D. 수열과의 관계 [고2-수학1]

 

 

 

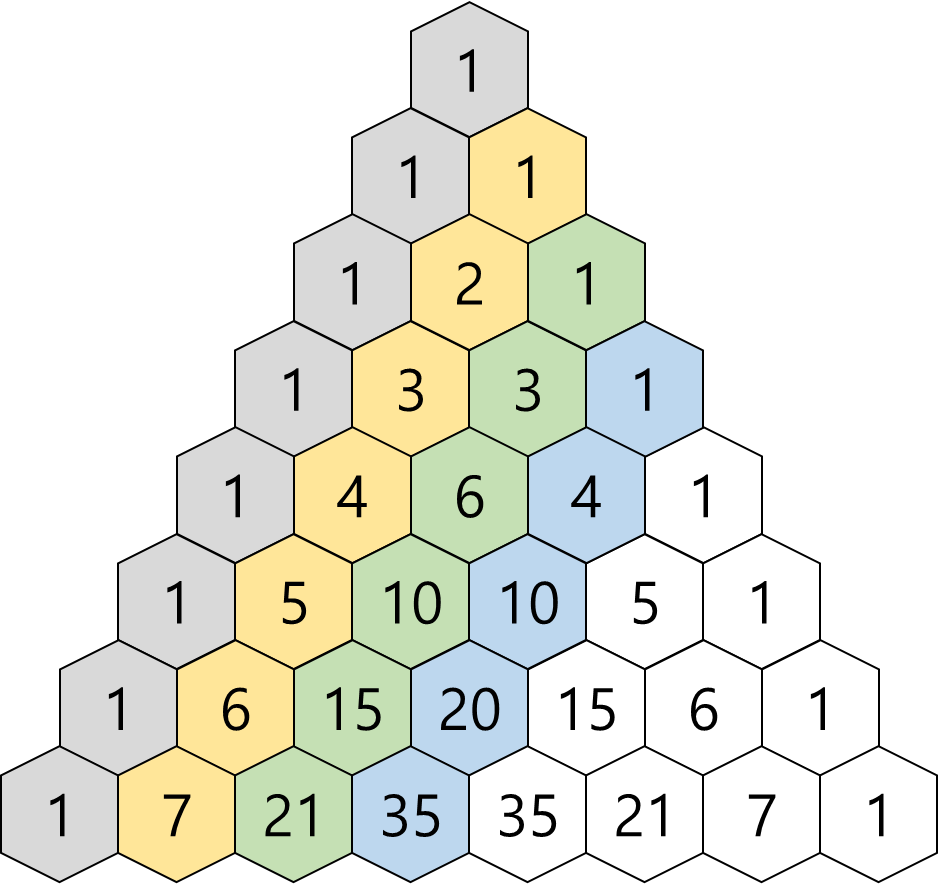
① 각 줄에서  $n$ 번째 수들을 이어서 보면 수열이 나온다.

 

 

각 줄에서의 2번째 수들을 이어서 보면

$1$,  $2$,  $3$,  $4$, ···

즉, 자연수의 수열입니다.

 

 

각 줄에서의 3번째 수들을 이어서 보면

$1$,  $3$,  $6$,  $10$, ···

수1에서 자주 보이는 계차수열이기도 하고,

삼각수의 수열이라고도 합니다.

 

 

 

 

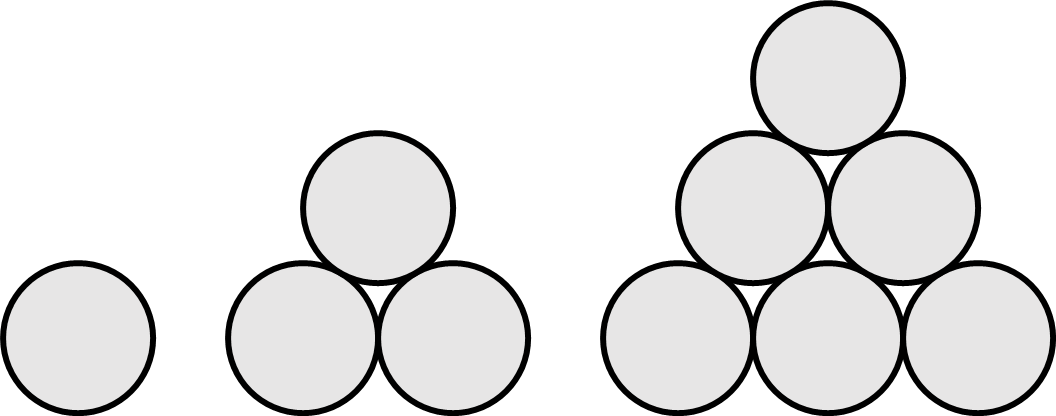
삼각형 모양으로 공을 쌓을 때

필요한 공의 수라고 생각할 수 있죠.

 

 

② 하키스틱(Hockey stick) 법칙

각 숫자는 바로 위 수열의 합을 나타낸다는 법칙입니다.

 

 

 

 

$1+2+3+4+5+6=21$

$1+4+10+20=35$

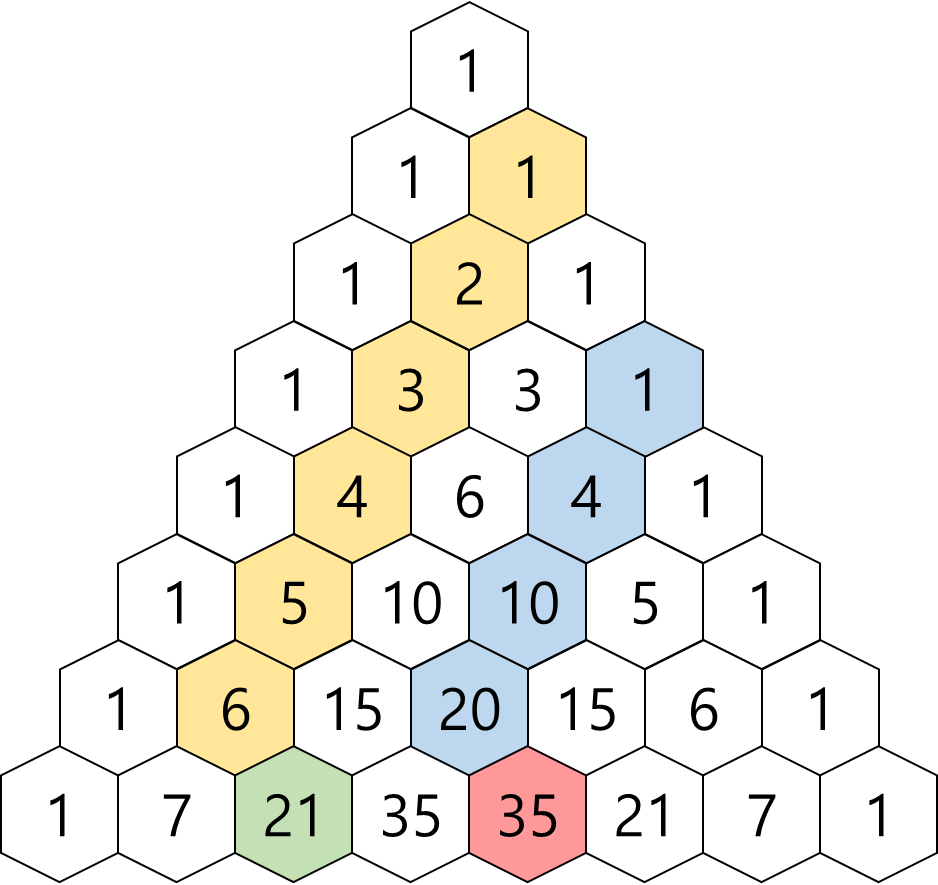
이렇게 말이죠.

 

 

이 모양이 마치 하키스틱 같아서

하키스틱 법칙이라고 한답니다.

 

 

 

마무리

 

이 외에도 성질이 더 있지만

이미... 충분히 많죠?

고등수학을 공부하면서 조금이라도

도움이 될 만한 성질들에 대해 알아봤어요.

여기까지!