■ 목표
- 곱셈공식 변형해보기
- 문제에서 잘 활용해보기

개요
<참고>

지난 번 알아봤던 10개의 곱셈공식 중
딱 4개만 형태를 바꿔보려고 해요.
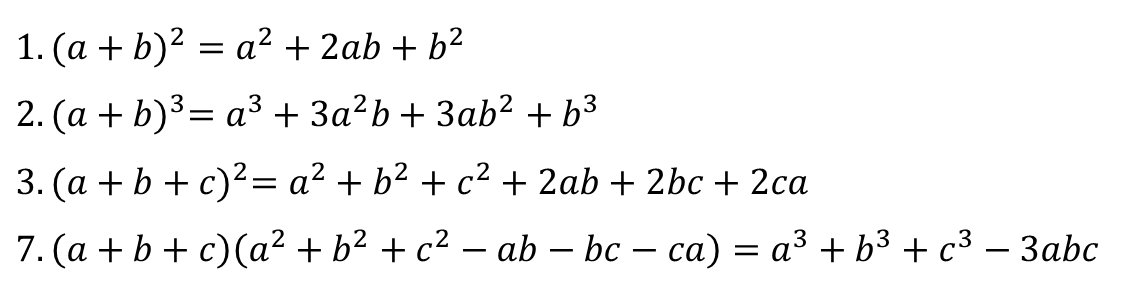

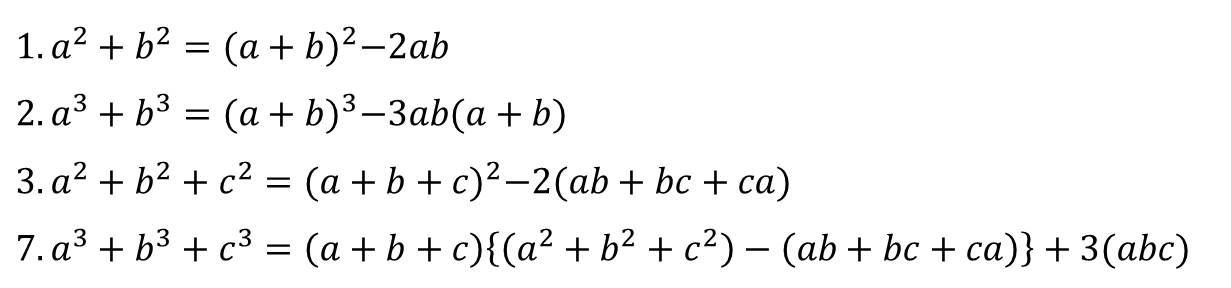
약간 '순서를 바꾼 것 뿐' 이지만
바꾼 이유가 있겠죠?
곱셈공식의 변형
■ 1번 공식



공식을 살펴보면 안에 여러 작은 식들이 보입니다.
이를 색으로 한번 구분지어 볼게요.
① 빨간색은 "두 수의 합", "두 수의 곱" 처럼
자주 사용되고 쉬운 연산식이에요.
② 파란색은 "두 수의 제곱의 합" 처럼
어렵고 상대적으로 흔하지 않은 연산식이죠.
문제를 만드는 입장에서는 보통
"쉬운 식을 알려줄테니 어려운 식을 구해보시오."
라고 출제하기 때문에,
공식을 "문제를 풀기에 좋은 형태" 로 바꾸는 것입니다.
다시 살펴볼까요?

결과를 말로 설명해보면
"두 수의 합과 두 수의 곱만 알고 있으면 제곱의 합을 구할 수 있다!"
라고 할 수 있습니다.
■ 2번 공식



가운데 두 항이 복잡해보였지만,
공통인 $3ab$ 를 묶었더니
쉬운 계산식들이 나왔죠.
이를 이용해 정리하면 됩니다.
두 수의 합과 두 수의 곱만 알고 있으면
이번엔 세제곱의 합을 구할 수 있다는 걸 알았습니다.
■ 3번 공식
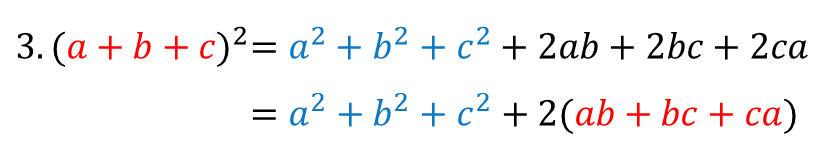

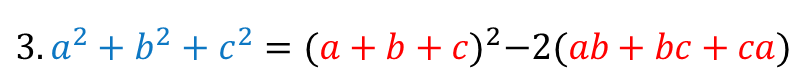
음 생각보단 별 거 없죠?
■ 7번 공식



이렇게 됩니다.
제곱의 합 즉, $a^2+b^2+c^2$ 이라는 항도
물론 조금 까다로울 때가 있지만
위의 3번 식을 보면, 생각보다는 금방 구할 수 있겠다는 생각이 들죠?
마무리
여기까지!
공식의 활용은 문제를 많이 풀어보면서
외운다기보단 익숙해진다는 느낌이 좋을 것 같아요!
다음은 다항식의 나눗셈에 대해 알아볼게요.
'공통수학1 [고1] > 1. 다항식의 연산' 카테고리의 다른 글
| 나눗셈에 대한 등식 (2) | 2022.09.23 |
|---|---|
| 파스칼의 삼각형 [심화] (0) | 2022.09.23 |
| 곱셈공식 원리(3/3) C. 변수와 상수가 구분되는 경우 (0) | 2022.09.23 |
| 곱셈공식 원리(2/3) B. 동류항이 소거되는 경우 (2) | 2022.09.23 |
| 곱셈공식 원리(1/3) A. 동류항이 합쳐지는 경우 (0) | 2022.09.23 |





댓글