■ 목표
- 인수 vs 약수 차이 이해하기
- 인수정리 이해하기

인수 vs 약수
"소인수분해", "인수분해"
뭔가 자연스럽게 사용은 하고 있었지만
인수가 정확히 뭘까요?
인수(Factor)는 약수(Divisor)와
비슷한 단어이긴 합니다.
하지만, 사용하는 곳이 조금 다를 뿐이죠.
예를 들어, $4$는 $12$를 나눌 수 있습니다.
$12÷4=3$
이때, $4$를 $12$의 약수라고 합니다.
한편, $4$는 $3$을 곱해서 $12$를 만들 수 있습니다.
다른 말로,
$12$를 "$4$와 $3$의 곱으로 표현" 할 수 있습니다.
$12=4×3$
이때는, $4$를 $12$의 인수라고 합니다.
사실 거의 별 차이는 없지만,
약수는 "어떤 수를 나눌 수 있는 수"
인수는 "어떤 수를 구성하는 요소인 수"
라는 의미로 사용합니다.
고등수학에서 나눗셈을 할 때는,
나눗셈(÷)이라는 "연산과정" 의 의미보다
"등호(=)" 의 의미에 좀 더 집중합니다.
<참고> [고1 수학/1. 다항식의 연산] - 나눗셈에 대한 등식

따라서, 자연스럽게
약수보다는 인수라는 단어를 많이 사용하게 됩니다.
인수정리
다시 등장한 나눗셈에 대한 항등식

그동안은 다항식의 나눗셈을 하면서
"나머지" 를 구하는 방법에 대해 계속 알아봤었죠.
하지만, "나머지가 0" 혹은 "나누어 떨어졌다" 인 경우.
즉, 나머지인 $R(x)$ 이 사라지면 식은 이렇게 됩니다.

$A(x)$ 는 $B(x)$ 와 $Q(x)$ 의 곱으로 이루어졌다.
즉, $B(x)$ 와 $Q(x)$ 는 $A(x)$ 의 인수입니다.
또, 이 식은 항등식이기 때문에
$B(x)$ 의 근을 이용해서, $A(x)$ 근을 찾을 수 있습니다.
양변에 $B(x)$ 를 $0$이 되게 하는
$x$를 대입하는 것이죠.
■ 예시
이차식 $x^2-5x+6$ 이 $(x-2)$ 로 나누어 떨어진다.
식으로 써보면, 이렇게 되겠죠.

오른쪽 식에서 $x=2$ 를 대입하면 $0$ 이기 때문에,
왼쪽 식에도 $x=2$ 를 대입하면 $0$ 일 거라는 것을
알 수 있습니다.
■ 인수정리

인수정리를 이용해 미정계수 구하기
인수정리를 이용한 문제 유형입니다.
$A(x)$ 의 인수인 $B(x)$ 를 보면
쉽게 근을 찾을 수 있다는 점을 이용합니다.
■ 일차식인 $B(x)$ 로 나누어 떨어진 경우
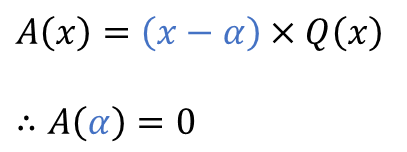
■ 이차식인 $B(x)$ 로 나누어 떨어진 경우
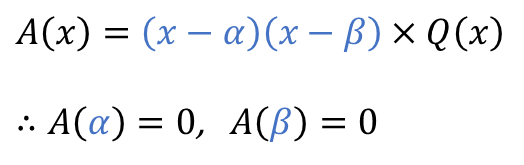
예제로 미정계수 찾는 문제를 하나 풀어볼까요?
■ 예제
다항식 $x^3+x^2+ax+b$ 가 $x^2-1$로 나누어 떨어질 때, 상수 $a$와 $b$에 대하여 $a+b$ 를 구하시오.
(풀이)
식을 세워보면 이렇습니다.
$x^3+x^2+ax+b=(x^2-1)Q(x)$
$x^3+x^2+ax+b=(x+1)(x-1)Q(x)$
즉, $x=-1$, $x=1$ 을 대입해 보면
$-1+1-a+b=0$, $1+1+a+b=0$ 임을 알 수 있습니다.
연립해서 풀어보면 $a=-1$, $b=-1$ 이므로,
$a+b=-2$ 입니다.
마무리
여기까지!
다음 대단원인 인수분해 단원에서는
인수정리를 이용한 인수분해 방법을
다룰 수 있을 거예요.
'공통수학1 [고1] > 2. 항등식과 나머지정리' 카테고리의 다른 글
| 나머지정리2 [3차식으로 나눈 나머지] (0) | 2022.11.11 |
|---|---|
| 몫과 나머지의 변형 (0) | 2022.11.08 |
| 나머지정리1 [1차식/2차식으로 나눈 나머지] (0) | 2022.11.07 |
| 나눗셈에 대한 항등식 (0) | 2022.11.06 |
| 항등식의 풀이 - B. 수치대입법 (0) | 2022.10.10 |





댓글