■ 목표
- 항의 개수 추리하기
- 특정 항의 계수 구하기

개요
전개하는 것이 어렵진 않지만,
직접 모든 항을 전개하기에는 한계가 있는 경우도 있습니다.
항이 엄청 많은 식을 곱한다거나,
여러 개의 식을 동시에 곱한다거나 하는 경우죠.
그래서 전부 전개를 하지 않고도
필요한 정보를 알아내는 연습을 해보려고 합니다.
항의 개수 추리하기
전개했을 때 나오게 될 전체 항의 개수는
서로 곱해지는 식들의 안에
"항이 총 몇 개 있는지" 만 알면 됩니다.
원리는 이렇습니다.
■ 예시1
Q. 이 식을 전개했을 때 나오는 항 중에서 아무거나 하나를 쓰시오.

이 문제의 답을 생각해 보면
답은 4가지 중 하나입니다.
첫 번째 식에서는 $a$ 또는 $b$ 둘 중 하나
두 번째 식에서는 $c$ 또는 $d$ 둘 중 하나를 골라
서로 곱하면 되죠.
이는 경우의 수 문제와 동일하게 생각할 수 있습니다.
식은 주머니로, 식 안의 항들은 구슬로 생각하면
문제는 이렇게 됩니다.
Q. 각 주머니에서 구슬을 하나씩 빼는 경우의 수는?

A. 2가지 × 2가지 = 4가지
그래서 전개했을 때, 항의 개수도 4개입니다.
같은 원리로,
항이 많아지거나, 식이 많아지더라도
어렵지 않게 항의 개수는 구할 수 있습니다.
■ 예제1
Q. 다음 식을 전개했을 때, 전체 항의 개수는?
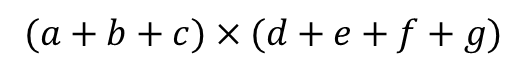
(정답)
첫 번째 주머니에서 3개의 구슬 중 하나
두 번째 주머니에서 4개의 구슬 중 하나를 뽑는 경우의 수는
→ $3×4=12$ 가지
■ 예제2
Q. 다음 식을 전개했을 때, 전체 항의 개수는?

(정답)
4개의 주머니에서 각각 2개의 구슬 중 하나씩 뽑는 경우의 수는
→ $2×2×2×2=16$ 가지
하지만 동일한 변수(문자)가 있는 식에서는
항의 개수가 조금 다를 수 있습니다.
동류항이 생기기 때문이죠.
■ 예시2

이 식도 전개하면 물론 4개의 항이 나오지만,

$x$ 와 상수항이 곱해진 두 항
$3x$ 와 $2x$ 는 동류항입니다.

즉, 정리를 하고 나면 항이 3개인 식이 되죠.
그래서 실제로 문제에서는
"전개했을 때, 전체 항의 개수" 보다는
"$x$ 항의 계수" 를 자주 물어봅니다.
특정 항의 계수 찾기
그럼 전개를 전부 하지 않고도
동류항이 몇 개나 나오는지 알 수 있을까요?

아까의 식에서는 $x$ 항이 2개가 나왔죠.
바로 $3x$ 와 $2x$ 입니다.
이 두 항은 $x$ 가 하나만 곱해지는 항이므로,
두 식 중 하나에서만 $x$ 를 뽑아야 합니다.
그리고 나머지 식에서는 상수항을 뽑아야 하죠.
순서대로
$x$ 와 $3$ 을 뽑거나
$2$ 와 $x$ 를 뽑는 것입니다.

$x$ 를 하나만 뽑는 방법이 두 가지이므로,
2개의 동류항이 나올 거라는 것도 알 수 있죠.
■ 예제3
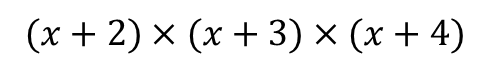
1. $x^2$ 항의 계수를 구하시오.
2. $x$ 항의 계수를 구하시오.
(정답)
1. $x$ 가 2개 필요하기 때문에, 2개의 $x$ 를 어디서 뽑을지
그리고 1개의 상수는 어디서 뽑을지를 선택해 주면 됩니다.
각 식에서 순서대로
$2$, $x$, $x$ 를 뽑으면 → $2x^2$
$x$, $3$, $x$ 를 뽑으면 → $3x^2$
$x$, $x$, $4$ 를 뽑으면 → $4x^2$
A. $(2+3+4)x^2$ 이므로 계수는 $9$ 입니다.
2. $x$ 가 1개 필요하기 때문에, 1개의 $x$ 를 어디서 뽑을지
그리고 2개의 상수는 어디서 뽑을지를 선택해 주면 됩니다.
각 식에서 순서대로
$x$, $3$, $4$ 를 뽑으면 → $12x$
$2$, $x$, $4$ 를 뽑으면 → $8x$
$2$, $3$, $x$ 를 뽑으면 → $6x$
A. $(12+8+6)x$ 이므로 계수는 $26$ 입니다.
"필요한 1개를 어디서 뽑을지" 를 생각해 보면
좀 더 쉽게 찾을 수 있겠죠?
마무리
여기까지!
다음 시간에는 곱셈공식에 대해서 알아볼게요.
'공통수학1 [고1] > 1. 다항식의 연산' 카테고리의 다른 글
| 곱셈공식 원리(1/3) A. 동류항이 합쳐지는 경우 (0) | 2022.09.23 |
|---|---|
| 곱셈공식 (0) | 2022.09.07 |
| 다항식의 곱셈 (0) | 2022.09.04 |
| 다항식의 덧셈과 뺄셈 (0) | 2022.09.02 |
| 식 (0) | 2022.08.31 |





댓글