반응형
■ 목표
- 분배법칙 이해하기
- 전개의 원리 이해하기

분배법칙
분배법칙은 분명
처음 배우는 개념은 아닐거예요.
덧셈과 곱셈이 섞인 계산에서 정의되는 법칙으로
다항식의 곱셈에서 가장 기본이 됩니다.
곱셈은 "여러번 더하기" 라는 의미입니다.
3을 곱한다는건 3번 더하라는 말과 같죠.
■ 예시
예를 들어, $3 \times (a+b)$ 를 계산하는 과정은
다음과 같습니다.

마치, $3×$ 라는 계산을
$a$ 와 $b$ 에게 평등하게 "분배" 해준 것 같죠.
그래서 분배법칙은
다음과 같은 직관적인 이미지로 이해하는 것도 중요합니다.
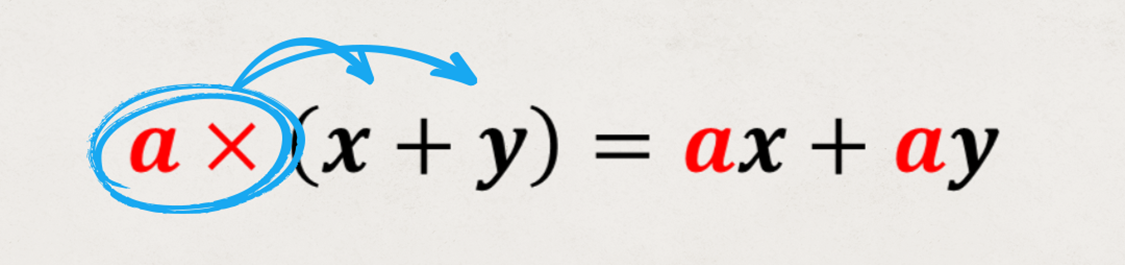
다항식의 곱셈(전개하기)
이번엔 식과 식을 곱합니다.
예시로, $(x+y)$ 에 $(a+b)$ 라는 식을 곱해볼거에요.
이때, 곱하는 식을 A로 치환해보면
어떤 과정인지 더 눈에 잘 보일거예요.
■ 예시

결과는 $a$ 와 $b$, $x$ 와 $y$ 가
한번씩 평등하게 곱해진
총 4개의 항이 나왔죠.
결국 두 식을 곱한다는 건,
각 식이 가진 모든 항을 서로 곱해서 나열하는 것입니다.
괄호를 모두 풀어서, "모든 항들을 풀어놓는다"
그래서 이 과정을 전개한다고합니다.

마무리
여기까지!
다음은 전개에 대해서 조금 더 깊게 살펴보도록 해요.
반응형
'공통수학1 [고1] > 1. 다항식의 연산' 카테고리의 다른 글
| 곱셈공식 (0) | 2022.09.07 |
|---|---|
| 다항식의 곱셈 - 전개의 원리 (0) | 2022.09.05 |
| 다항식의 덧셈과 뺄셈 (0) | 2022.09.02 |
| 식 (0) | 2022.08.31 |
| 항 (0) | 2022.08.30 |





댓글