■ 목표
- $i$의 거듭제곱의 표현
- 복소수의 거듭제곱의 표현
- 복소수의 곱셈과 나눗셈의 표현

$i$의 거듭제곱의 표현
지난번에 두 가지 내용에 대해 배웠습니다.
① 복소수를 복소평면에 표현하기
② 직교좌표를 극좌표로 표현하기
이를 통해 "$i$의 거듭제곱" 이 갖는
기하학적 의미에 대해 알아보려고 해요.
허수단위 $i$는 $0+1·i$
즉, 실수부가 $0$, 허수부가 $1$인 복소수이므로,
복소평면 위의 점 $(0, 1)$에 대응됩니다.
마찬가지로,
$i^2=-1=-1+0·i$ → 점 $(-1, 0)$
$i^3=-i=0-1·i$ → 점 $(0, -1)$
$i^4=1=1+0·i$ → 점 $(1, 0)$
이렇게 대응되죠.

이 직교좌표를
원점으로부터 거리와 각도를 이용해
극좌표로 바꾸면 다음과 같습니다.

이때, 신기하게도
네 점은 원점으로부터의 거리가 모두 $1$이고,
각도만 $90^\circ$ 씩 차이가 난다는 걸 알 수 있죠.
그래서, $i\times i=i^2$ 이라는 건,
복소평면에서는
$(1, 90^\circ)\times(1, 90^\circ)=(1, 180^\circ)$
라는 의미입니다.

즉, $i$의 거듭제곱의 기하학적 표현이란
$i$ 를 곱할 때 마다 $90^\circ$ 씩 회전하는 회전이동을 의미합니다.
복소수의 거듭제곱의 표현
이번엔 일반적인 "복소수의 거듭제곱" 에서도
회전이동의 의미를 갖는지 확인해보려 합니다.
■ 예시
복소수 $z=1+i$ 를 복소평면에 나타내면 다음과 같습니다.
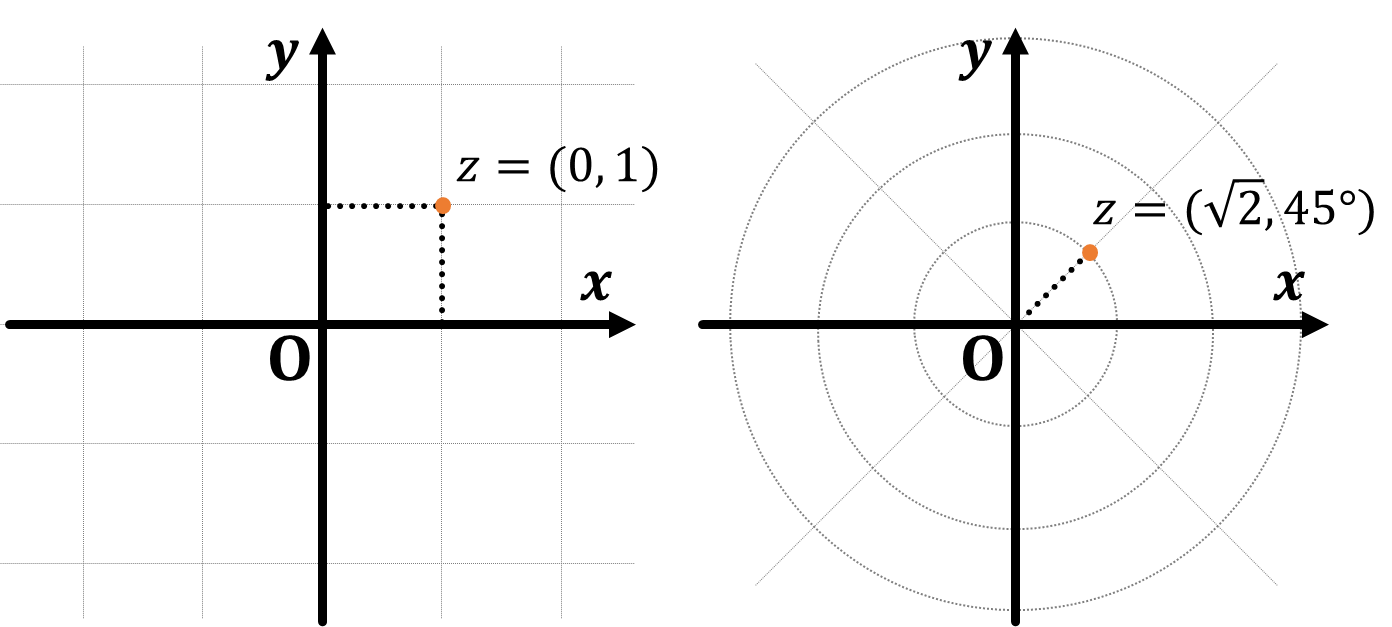
이제, 거듭제곱입니다.
$z^2=(1+i)^2=2i$
$z^3=(1+i)^3=2i(1+i)=-2+2i$
좌표로 표현하면,
직교좌표 $(0, 2)$ → 극좌표 $(2, 90^\circ)$
직교좌표 $(-2, 2)$ → 극좌표 $(2\sqrt{2}, 135^\circ)$
이를 복소평면에 나타내면 다음과 같습니다.
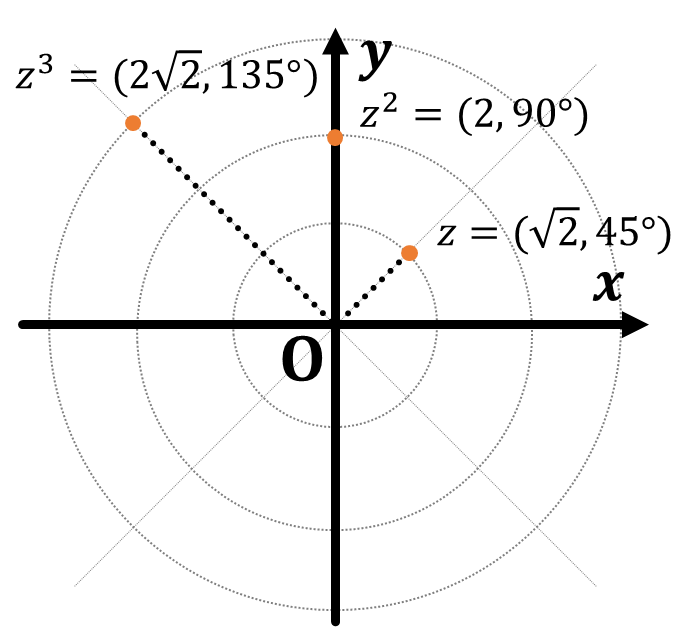
각도가 $45^\circ$ 씩 증가할 뿐만 아니라,
원점으로부터의 거리도 $\sqrt{2}$배가 되는 것을 확인할 수 있죠.
이 성질을 다음과 같이 한 줄로 정리할 수 있습니다.
■ 복소수의 거듭제곱의 기하학적 표현

복소수를 한 번씩 곱할 때마다,
거리는 계속 곱해지고, 각도는 계속 더해지는 거죠.
※ 이때, 원점으로부터의 거리가 $1$ 인 경우,
거듭제곱을 해도 거리는 항상 $1$ 이 됩니다.
이 경우에 대해 공식으로 정리된 것이
"드 무아브르 공식(de Moivre’s formula)" 입니다.
삼각함수를 이용한 일반각에 대한 이해가 필요하기 때문에
여기서는 넘어가도록 할게요.
■ 예제
$z_1=\frac{1+i} {\sqrt{2}}$, $z_2=\frac{1+\sqrt{3}i} {2}$ 라 할 때, ${z_1}^n={z_2}^n$ 을 만족시키는
가장 작은 자연수 $n$ 의 값을 구하시오.
(풀이)
정답 : $n=24$
두 복소수의 극좌표를 구해보면 다음과 같습니다.
$z_1=(1, 45^\circ)$, $z_2=(1, 60^\circ)$
두 복소수 모두 원점과의 거리가 $1$ 이기 때문에,
거듭제곱을 해도 거리는 멀어지지 않고 회전이동만 하게 됩니다.
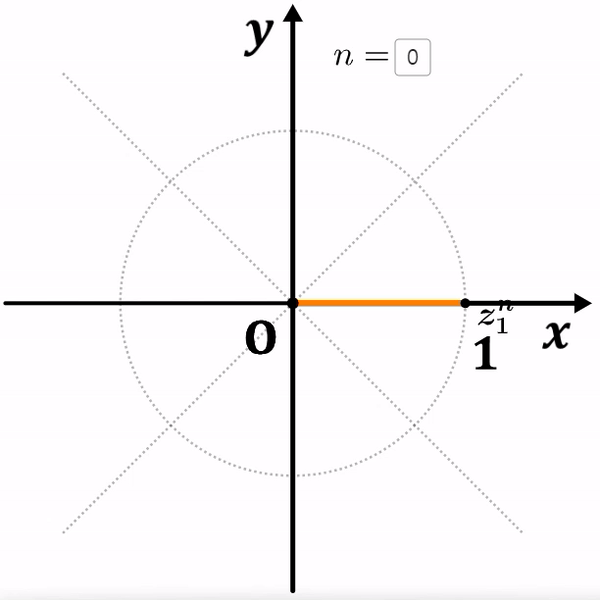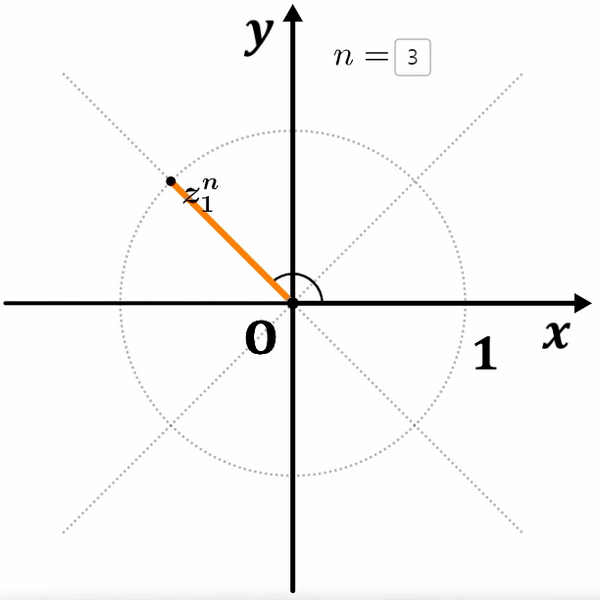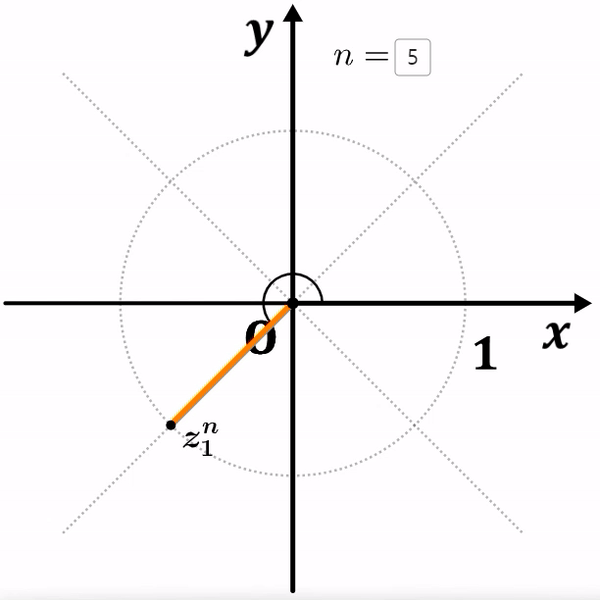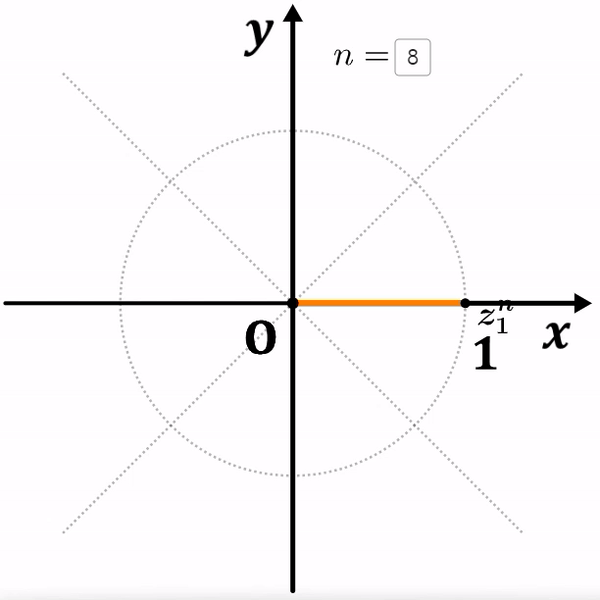
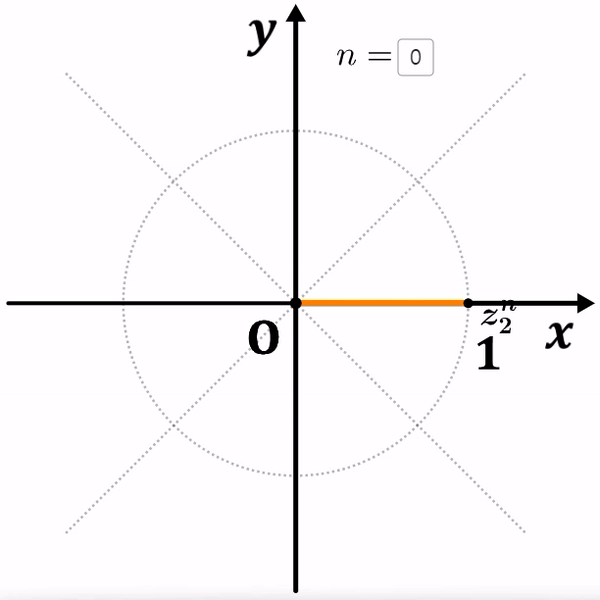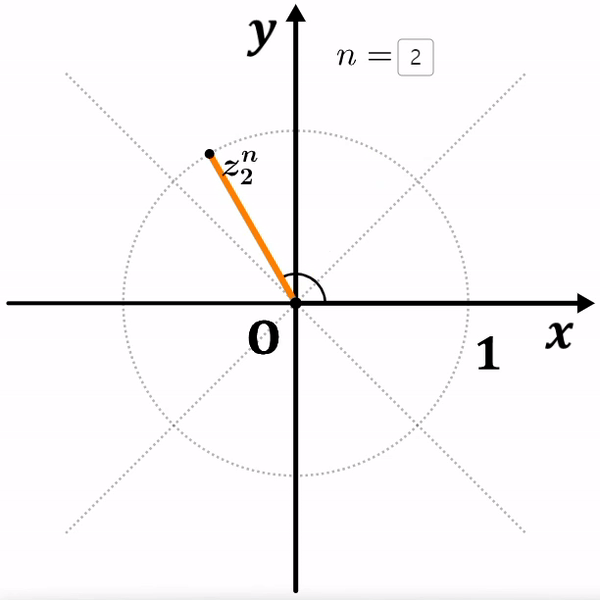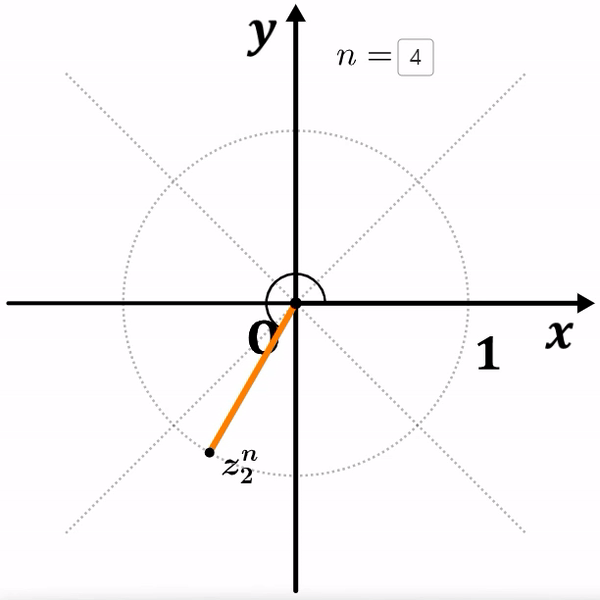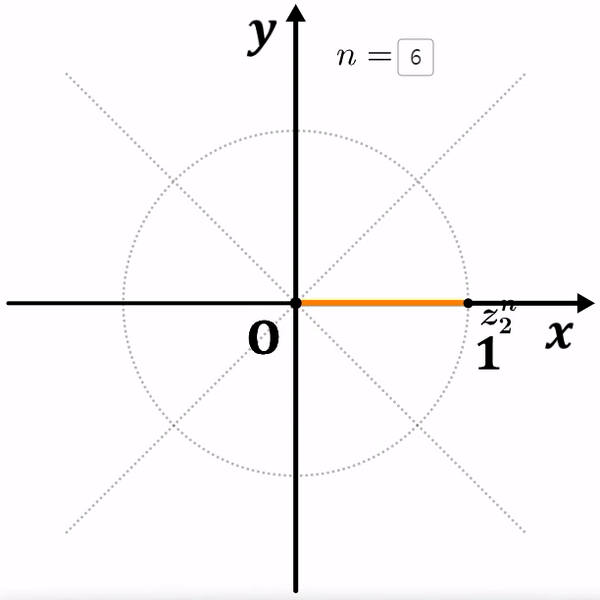
여기서 ${z_1}^8=1$ 이고, ${z_2}^6=1$ 이 되는 것을 알 수 있습니다.
따라서, $8$ 과 $6$ 의 최소공배수인
$n=24$ 일 때 처음으로 같아지게 됩니다.
복소수의 곱셈과 나눗셈의 표현
극좌표의 회전이동을 이용한 복소수의 거듭제곱은
특수각이라는 특정상황에서 꽤 큰 도움이 됩니다.
서로 다른 두 복소수의 곱셈과 나눗셈에서도
같은 원리가 적용이 되는데,
거리는 곱하거나 나누고, 각도는 더하거나 빼주면 됩니다.
■ 복소수의 곱셈과 나눗셈의 기하학적 표현

■ 예시1
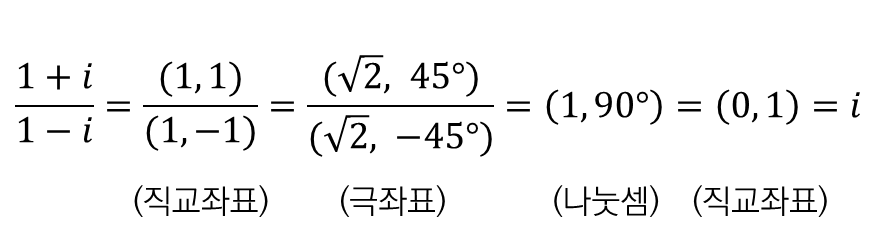
■ 예시2
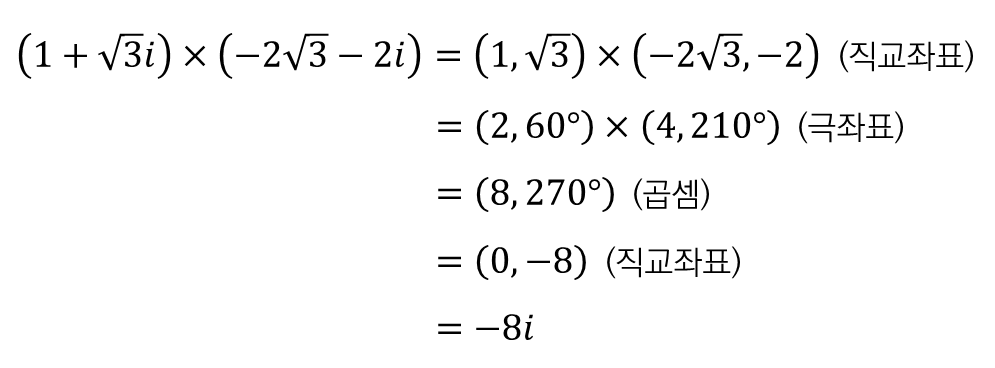
마무리
정확한 증명을 제외하고
추상적으로 보이는 성질로만 살펴본 내용이라 많이 어려웠을 수도 있어요.
그래도 여기까지 열심히 봤다면
분명 큰 도움이 되었을 거라 생각해요!
'공통수학1 [고1] > 4. 복소수' 카테고리의 다른 글
| 복소수의 곱셈[심화](2/3) - 좌표계(Coordinate System) (0) | 2023.05.27 |
|---|---|
| 복소수의 곱셈[심화](1/3) - 복소평면(Complex Plane) (0) | 2023.05.23 |
| 조건을 만족하는 복소수 찾기[심화](2/2) - 이차방정식 이용 (0) | 2023.05.17 |
| 조건을 만족하는 복소수 찾기[심화](1/2) - 켤레복소수의 성질 이용 (2) | 2023.05.13 |
| 식을 만족하는 복소수 찾기 (0) | 2023.05.06 |





댓글