■ 목표
- $f(z)$ 가 실수일 조건
- A. $f(z)$ 를 하나의 복소수로 표현하기
- B. 켤레복소수의 성질 이용하기
![조건을 만족하는 복소수 찾기[심화] 썸네일](https://blog.kakaocdn.net/dn/CJFVV/btsfpevxGI9/p4uXx1jAiwwMZSzMZzfxxK/img.png)
$f(z)$ 가 실수일 조건
특정 $z$ 를 찾아내는 유형에 대해 2가지를 배웠습니다.
"$z$ 가 실수" 라는 조건이 있다면, 허수부분인 $b=0$ 임을 이용하고,
조건을 만족하는 복소수 찾기
■ 목표 - 조건을 만족하는 $z$ 찾기 - $z$가 실수일 조건 - $z$가 순허수일 조건 조건을 만족하는 복소수 $z$ 찾기 어떤 모르는 복소수를 문자로 놓을 때 $z$ 를 사용하기로 했죠. 그리고 복소수는 실
indv-wrappedmath.tistory.com
"$z^2-3z=1+i$" 라는 식이 있다면,
실수부분, 허수부분을 비교해서 $z$ 를 찾아낼 수 있었죠.
식을 만족하는 복소수 찾기
■ 목표 - 복소수 방정식 풀기 - A. 식을 하나의 복소수로 만들기 - B. 식을 하나 더 만들기 복소수 방정식 풀기 주어진 식을 만족하는 복소수 찾기. 이것은 방정식을 푼다는 것입니다. 예를 들어, $
indv-wrappedmath.tistory.com
이번 유형은 마치 두 유형을 섞은 듯한
복잡한 조건이 등장합니다.
$f(z)$ 가 실수이기 때문에, 허수부분은 $0$ 이지만,
$f(z)$ 가 복잡하기 때문에, 허수부분을 바로 찾아내기는 쉽지 않죠.
예를 들면, 다음과 같습니다.
■ 예시

이제 이 문제를 3가지 방법으로 풀어보려고 합니다.
A. $f(z)$ 를 하나의 복소수로 표현하기
$z=a+bi$ 를 대입함으로써
주어진 식의 실수부분과 허수부분을 찾아보려고 합니다.
■ 예시

① $z=a+bi$ 대입

② 분모의 실수화

이게 맞나 싶은 순간이 한두 번이 아닙니다만,
어쨌든 분모의 허수를 없애고
실수부분과 허수부분을 구분해 냈습니다.
③ 허수부분=0

어차피 분모는 확실히 양수이므로,
분모만 $0$ 이 되면 됩니다.
문제에서 $z=a+bi$ 는 허수이므로,
$b$ 는 $0$ 이 아닙니다.
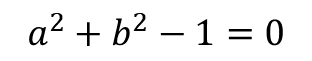
따라서, 구하고자 하는 답은 이렇게 됩니다.
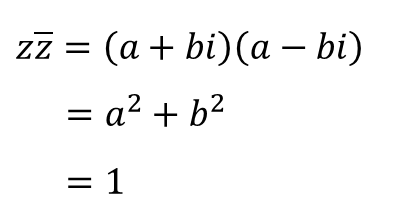
B. 켤레복소수의 성질 이용하기
켤레복소수는 허수부분의 부호만 반대입니다.
그러니 어떤 실수의 켤레복소수는 아무것도 변하는 게 없죠.
예를 들면, $\overline{3}=3$ 입니다.
■ 예시

① $\overline{f(z)}=f(z)$
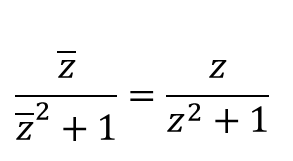
② 식을 정리한다.
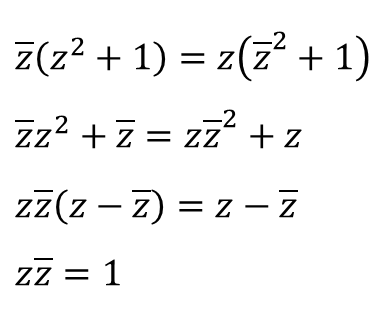
잉? 벌써 끝입니다.
압도적인 풀이과정의 차이가 보이죠.
마무리
특정 $z$ 를 구해야 하는 문제에서
$z=a+bi$ 를 무작정 대입하는 것은 좋은 방법이 아닙니다.
왜 이 문제를 냈을까?
어떤 성질을 이용하면 좋을까?
고민해 보면 더 좋은 풀이가 생각날 수 있답니다.
다음엔 한 가지 또 다른 관점에서의 풀이를 보여드릴게요!
'공통수학1 [고1] > 4. 복소수' 카테고리의 다른 글
| 복소수의 곱셈[심화](1/3) - 복소평면(Complex Plane) (0) | 2023.05.23 |
|---|---|
| 조건을 만족하는 복소수 찾기[심화](2/2) - 이차방정식 이용 (0) | 2023.05.17 |
| 식을 만족하는 복소수 찾기 (0) | 2023.05.06 |
| 조건을 만족하는 복소수 찾기 (0) | 2023.05.01 |
| 음수의 제곱근 (0) | 2023.04.23 |





댓글