■ 목표
- 복소평면(Complex Plane)
- 복소수와 평면의 대응

개요
이번 내용의 최종목표는
"복소수의 곱셈의 기하하적 표현"입니다.
2015 교육과정 기준으로 고급수학I에 포함된 내용이라 접하기 쉬운 내용은 아니겠지만,
복소수의 곱셈원리에 대해 더 깊게 알 수 있는 좋은 내용입니다.
복소수를 나타낼 수 있는 평면과
평면좌표를 해석하는 두 가지 방법,
이를 통해 복소수의 곱셈원리까지 천천히 알아보도록 할게요.
복소평면(Complex Plane)
우리는 많은 계산과 문제들을 해결하기 위해 필요한 숫자들을
모두 찾아내면서 확장시켜 왔습니다.
<참고>
수 체계의 확장
■ 목표 - 수 체계의 확장 - 수 집합의 포함관계 수 체계의 확장 수 체계(Number System)는 우리가 배워온 모든 숫자들이 어떤 성질들을 가지는지, 어떤 연산이 가능한지 등을 연구한 것이에요. 그 과
indv-wrappedmath.tistory.com
그 과정에서 찾아낸 숫자들을 하나씩 선 위에 새겨 놓으면서,
마침내 모든 실수로 수직선 하나를 가득 채울 수 있다는 걸 알았죠.

하지만, 이후에 허수의 존재를 발견하면서 숫자는 복소수까지 확장됩니다.
그러고나니 복소수를 넣을 공간은 더 이상 수직선에 남아있지 않았죠.
복소수를 한번 살펴볼까요?

복소수는 실수부분과 허수부분으로 이루어져 있고,
$a$ 와 $b$ 는 모든 실수가 될 수 있습니다.
따라서, 복소수의 개수는
(실수 개수) $\times$ (실수 개수) 만큼 있고,
복소수를 전부 표현하려면 수직선이 두 개 필요합니다.
그렇게 만들어진
실수부분을 나타내는 수직선을 $x$ 축,
허수부분을 나타내는 수직선을 $y$ 축으로 한
이 평면을 복소평면 혹은 가우스평면이라고 합니다.

복소수와 평면의 대응
이제 모든 복소수를 복소평면에 나타낼 수 있습니다.
예를 들어, $z=1+2i$ 라는 복소수는
실수부분이 $1$, 허수부분이 $2$ 이므로,
복소평면 위의 점 $(1,2)$ 에 대응된다고 할 수 있죠.

만약, 실수부분이 $0$ 인 순허수라면, 전부 $y$ 축 위에 대응되고,
허수부분이 $0$ 인 실수라면, 전부 $x$ 축 위에 대응됩니다.
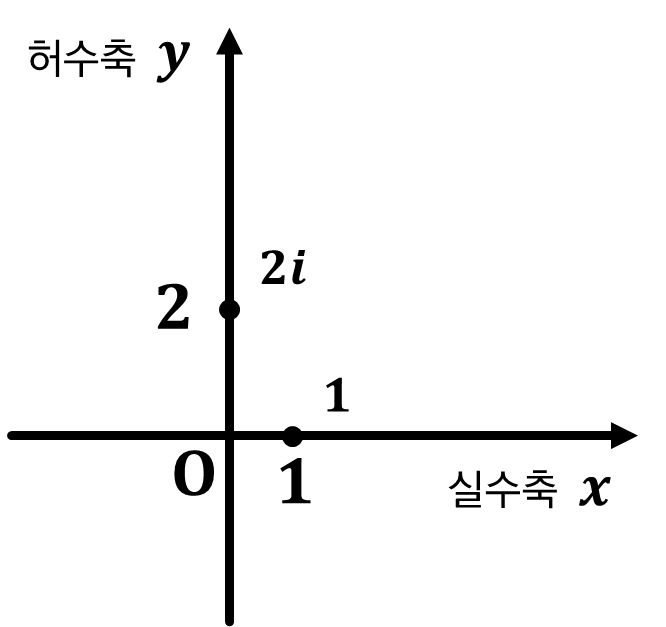
한 가지 주의할 점은
복소평면은 "복소수들을 위치로 표현한 것" 일 뿐,
실제 평면처럼 두 점 사이의 거리를 계산하거나
대소비교를 할 수는 없다는 것입니다.
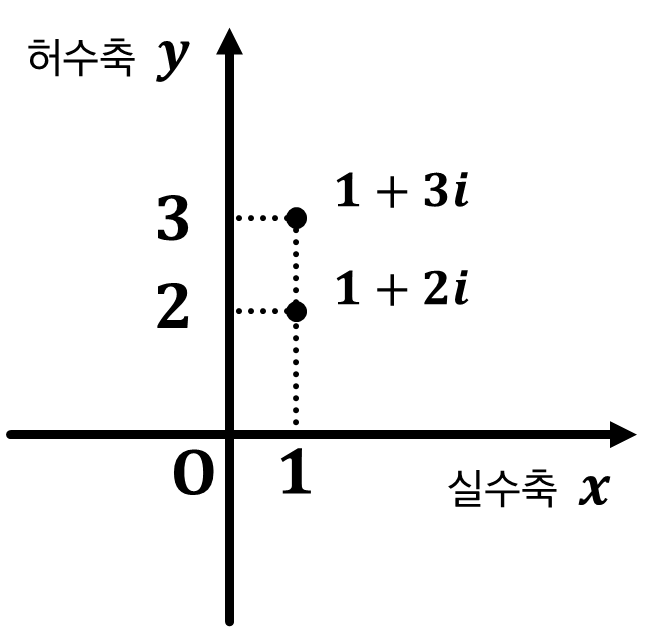
$1+3i$ 가 $1+2i$ 보다 위에 있다고 해서 더 크다는 뜻도 아니고,
둘 사이의 실제거리가 $1$ 이라는 것도 아닙니다.
그냥 편의상 $(1,2)$, $(1,3)$ 의 위치에 두 복소수가 있다고 보는 것이죠.
마무리
여기까지!
다음엔 좌표평면에 대해서 알아볼게요!
'공통수학1 [고1] > 4. 복소수' 카테고리의 다른 글
| 복소수의 곱셈[심화](3/3) - 기하학적 표현 (0) | 2023.06.04 |
|---|---|
| 복소수의 곱셈[심화](2/3) - 좌표계(Coordinate System) (0) | 2023.05.27 |
| 조건을 만족하는 복소수 찾기[심화](2/2) - 이차방정식 이용 (0) | 2023.05.17 |
| 조건을 만족하는 복소수 찾기[심화](1/2) - 켤레복소수의 성질 이용 (2) | 2023.05.13 |
| 식을 만족하는 복소수 찾기 (0) | 2023.05.06 |





댓글