■ 목표
- 조건을 만족하는
-
-

조건을 만족하는 복소수
어떤 모르는 복소수를 문자로 놓을 때
그리고 복소수는 실수부분과 허수부분으로 나누어져 있으니,
이제 조건을 하나 줄 테니
그리고 조건은 보통
어떤 복소수 "
"
■ 예제1
(정답)
쉽죠?
그래서 이 조건을 조금 다르게 표현해 볼 겁니다.
■ 예제2
사실 아무것도 달라진 게 없는 문제입니다.
왜 그럴까요?

"
우선 실수라면 허수부분이
양의 실수라고 했는데,
따라서,
결국, "
■ 예제3
이번엔 켤레복소수를 이용한 조건입니다.
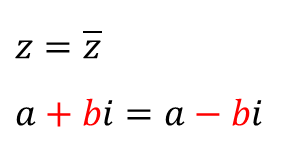
이 두 복소수가 같으려면,
즉, "
정리해 보면 다 똑같은 문제를
조건만 바꿔서 3가지 버전으로 낸 거죠.
그래서 우리는 "조건이 결국 무슨 뜻인지" 를 해석하는 연습이 필요합니다.
■

이번엔 복소수 "
"
■ 예제1
(정답)
■ 예제2
마찬가지로,

이번에는 음의 실수가 되어야 하므로,
즉, "
■ 예제3
조건을 살펴보면

결국,
"
■

마무리
가장 기본이 되는 것들을 정리해 보았어요.
다음엔 비슷하지만 조금 심화된 유형으로 찾아올게요!
'공통수학1 [고1] > 4. 복소수' 카테고리의 다른 글
| 조건을 만족하는 복소수 찾기[심화](1/2) - 켤레복소수의 성질 이용 (2) | 2023.05.13 |
|---|---|
| 식을 만족하는 복소수 찾기 (0) | 2023.05.06 |
| 음수의 제곱근 (0) | 2023.04.23 |
| 켤레복소수의 정의와 성질 (2) | 2023.04.16 |
| 복소수의 사칙연산과 거듭제곱 (0) | 2023.04.08 |





댓글