음수의 제곱근

■ 목표

- 음수의 제곱근 표현하기

- 음수의 제곱근의 성질

- 음수의 제곱근의 성질 활용 문제

 

 

 

 

 

음수의 제곱근

 

제곱근($\sqrt{ }$)을 처음 배웠을 때를 잠깐 돌이켜볼까요?

보통 루트라고 많이 부르지만, 제곱근이라고도 부릅니다.

따라서,  $\sqrt{2}$ 를  "루트 $2$"  또는  "제곱근 $2$" 라고 부르죠.

 

 

반면,  "$2$ 의 제곱근" 을 구하라는 건,  "제곱해서  $2$ 가 되는 근을 구하라" 는 뜻입니다.

식으로 나타내면 다음과 같죠.

$x^2=2$

따라서, 답은  $x=\pm \sqrt{2}$ 가 됩니다.

 

---

 

음수의 제곱근이라는 것은

제곱해서 음수가 되는 근을 구하라는 의미겠죠?

 

 

"$-2$ 의 제곱근" 을 구하라는 건,  "제곱해서  $-2$ 가 되는 근을 구하라" 는 뜻입니다.

$x^2=-2$

따라서, 답은  $x=\pm \sqrt{-2}=\pm \sqrt{2}i$ 가 됩니다.

 

 

 

음수의 제곱근의 성질

 

우리는  $\sqrt{-2}$,  $\sqrt{-3}$ 등의 음수의 제곱근들을 많이 찾아낼 수 있습니다.

이번엔 이 음수의 제곱근들끼리 계산을 해 볼 생각입니다.

 

 

우선, 덧셈과 뺄셈은 큰 의미가 없습니다.

$\sqrt{2}+\sqrt{3}$ 처럼

$\sqrt{2}i+\sqrt{3}i$ 도 $(\sqrt{2}+\sqrt{3})i$ 정도 외에는

더 이상 계산되지는 않을 테니까요.

 

 

하지만, 곱셈과 나눗셈은 어떨까요?

 

---

 

■ 곱셈

제곱근의 곱셈에서 다음과 같은 식이 성립함을 배웠습니다.

 

 

 

 

그래서  $\sqrt{2}\times \sqrt{3}=\sqrt{6}$ 이렇게 계산하면 되죠.

 

 

한쪽의 루트 안의 수가 음수이더라도 마찬가지로

$\sqrt{-2}$ $\times \sqrt{3}=\sqrt{-6}$

$\sqrt{2}\times \sqrt{-3}=\sqrt{-6}$

이렇게 계산이 가능하지만, 주의해야 하는 경우는

"둘 다 음수의 제곱근일 때" 입니다.

 

 

$\sqrt{-2}\times \sqrt{-3}=\sqrt{6}$

이렇게 계산하면 틀립니다.

이 과정을 자세히 살펴보면 다음과 같습니다.

 

 

 

 

음수의 제곱근을 두 개 곱한다는 뜻은

허수단위인  $i$ 가 두 개 곱해진다는 뜻이고,

즉,  $i^2=-1$ 이기 때문에, 결과에  $-1$ 이 생깁니다.

 

---

 

■ 나눗셈

이번엔 나눗셈입니다.

 

 

 

 

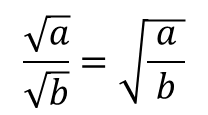
곱셈할 때처럼, 둘 다 음수의 제곱근이면

$-$ 가 생기지 않을까 싶겠지만,

이 경우는 조금 다릅니다.

 

 

 

 

허수단위인  $i$ 가 약분되어 사라지기 때문에,

그냥 계산한 결과와 같습니다.

 

 

나눗셈에서 주의해야 하는 경우는

"분모가 음수의 제곱근일 때" 입니다.

 

 

 

 

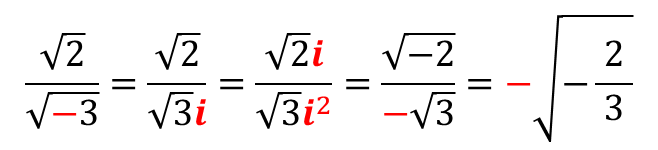
분모의 실수화를 하는 과정에서  $-1$ 이 생기는 것을 볼 수 있습니다.

 

 

음수의 제곱근의 곱셈과 나눗셈에서

주의해야 하는 경우에 대한 총정리입니다.

 

 

■ 음수의 제곱근의 성질

​

 

 

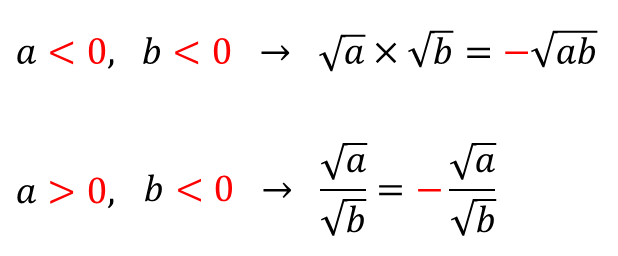
음수의 제곱근의 성질 활용 문제

 

위의 성질은  $a$,  $b$ 가 특정부호일 때만 성립하는 성질이다 보니,

계산보다는 반대로 부호를 물어보는 경우가 더 많은 편입니다.

 

 

■ 음수의 제곱근의 성질 활용

​

 

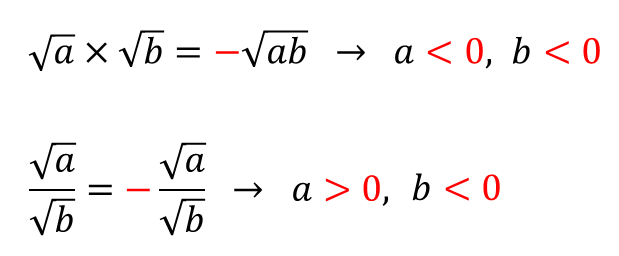
예제를 한번 풀어보는 것이 더 이해하기 쉬울 거예요.

 

 

 

■ 예제

Q. $0$ 이 아닌 세 실수  $a$,  $b$,  $c$ 에 대하여  $\sqrt{a}\sqrt{b}=-\sqrt{ab}$,  $\frac{\sqrt{c}}{\sqrt{b}}=-\sqrt{\frac{c}{b}}$ 일 때,  $\sqrt{a^2}+|b-c|$ 를 간단히 하시오.

(풀이)

$\sqrt{a}\sqrt{b}=-\sqrt{ab}$ 를 만족하는 경우는

$a$ 와  $b$ 모두 음수인 경우입니다.

 

$\frac{\sqrt{c}}{\sqrt{b}}=-\sqrt{\frac{c}{b}}$ 를 만족하는 경우는

$b$ 가 음수,  $c$ 가 양수인 경우입니다.

 

즉,  $a<0$,  $b<0$,  $c>0$ 이죠.

따라서,  $\sqrt{a^2}=|a|=a$,  $|b-c|=-(b-c)=-b+c$ 입니다.

$\therefore a-b+c$

 

 

 

마무리

 

여기까지!

이제 복소수에 대한 기본적인 개념들은 다 배운 셈이에요.

다음은 자주 나오는 몇 가지 유형 문제들에 대한 내용을 들고 찾아올게요!