복소수의 사칙연산과 거듭제곱

■ 목표

- 복소수의 사칙연산

- 복소수의 거듭제곱

 

 

 

 

 

복소수의 사칙연산

 

이제 두 복소수를 사칙연산($+,-,\times ,÷$) 해볼 텐데,

복소수에 실수부분과 허수부분이 있다는 사실만 잘 알고 있으면 됩니다.

 

 

 

 

그럼 사실  "복소수의 계산" 은 제곱근(루트)을 처음 배웠을 때 했던

"무리수의 계산" 과 똑같다는 걸 알 수 있죠.

$i=\sqrt{-1}$ 이므로, 허수도 결국은 제곱근이니까요.

 

---

 

■ 덧셈과 뺄셈

 

핵심은 끼리끼리입니다.

실수는 실수끼리, 허수는 허수끼리.

 

 

 

 

예를 들어, 무리수에서

$(2+\sqrt{2})+(3-3\sqrt{2})=5-2\sqrt{2}$ 인 것처럼,

 

 

복소수에서는

$(2+i)+(3-3i)=5-2i$ 이렇게 덧셈이 이루어집니다.

어렵지 않죠?

 

---

 

■ 곱셈

 

두 복소수가 모두 실수부분, 허수부분을 가지기 때문에

곱할 때는 분배법칙을 사용해야 합니다.

 

 

 

 

이때, 가장 중요한 것은  $i^2$ 입니다.

처음에 우리가  "제곱해서  $-1$ 이 되는 수" 를  $i$ 라 하기로 했죠.

따라서,  $i^2=-1$ 입니다.

 

---

 

■ 나눗셈

 

무리수의 나눗셈에서  "분모를 유리화" 하는 과정과 똑같습니다.

 

 

 

 

합차공식을 사용해서 분모에 있는 허수가 사라지게 해 주면 됩니다.

이 과정을  "분모의 실수화" 라고 합니다.

 

 

 

복소수의 거듭제곱

 

이번엔 허수단위인  $i$ 를 계속 곱해보려고 합니다.

 

 

 

 

$i^2=-1$ 이라는 중요한 허수의 성질로부터

$i^4=1$ 임을 찾아낼 수 있습니다.

 

 

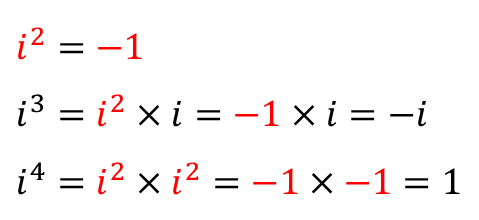
즉, 허수단위인  $i$ 는 아무리 많이 곱해도 결국은

"$i,-1,-i,1$ 중의 하나" 가 됩니다!

이 성질을 표현하면 다음과 같습니다.

 

 

■ 복소수의 거듭제곱

복소수의 거듭제곱

​

 

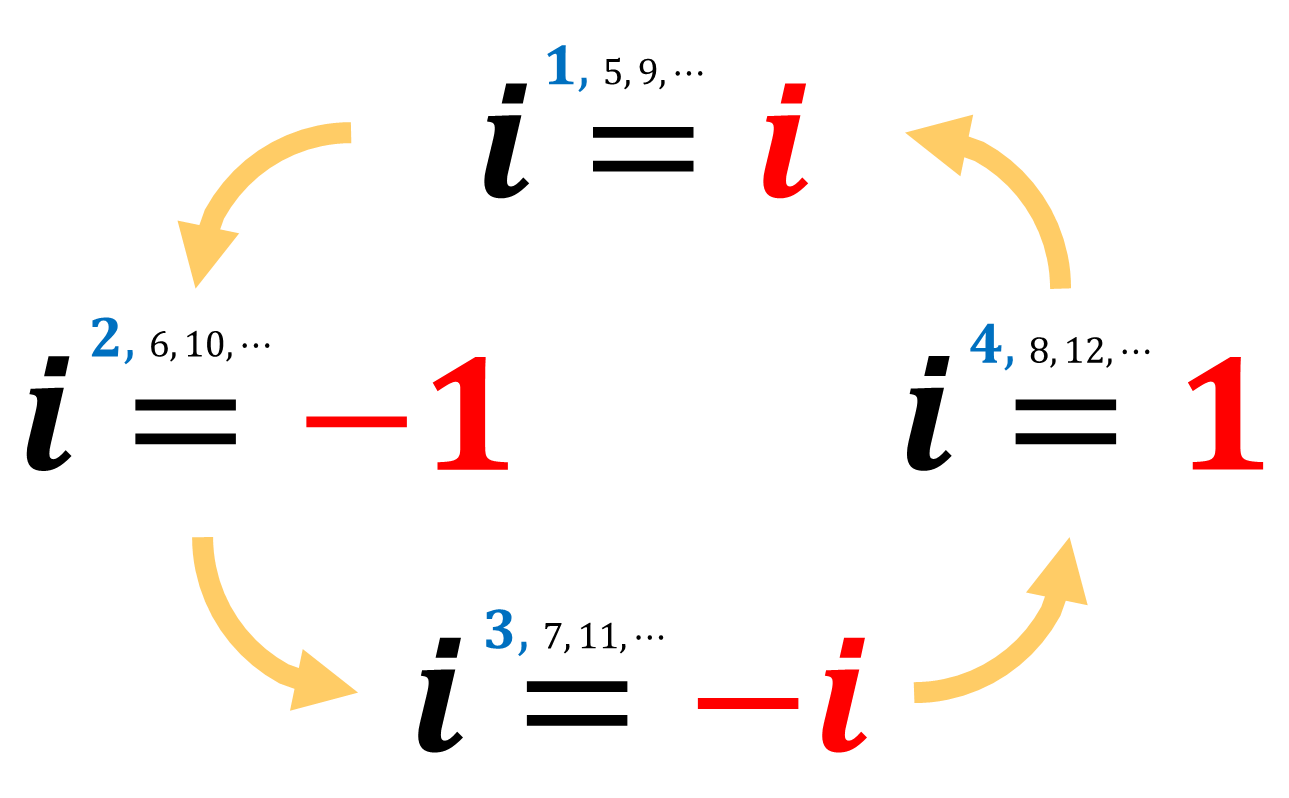
예를 들면,

$i^{10}=i^4\times i^4\times i^2=1\times 1\times (-1)=-1$ 이고,

$i^{100}=(i^4{)}^{25}=1^{25}=1$ 이 되는 거죠.

 

 

이처럼 복소수의 거듭제곱은

차수가 높아도, 보기보다 쉽게 풀리는 문제들이 많습니다.

 

 

 

■ 예제

Q. 다음 식을 간단히 하시오.

     $i+i^2+i^3+\cdots +i^{100}$

(풀이)

$i+i^2+i^3+i^4=i-1-i+1=0$

$i^5+i^6+i^7+i^8=i+i^2+i^3+i^4$

                                  $=i-1-i+1$

                                  $=0$

…

따라서, $0+0+0+\cdots +0=0$

 

 

 

마무리

 

복소수의 기본적인 연산들에 대해 알아봤어요.

원래 연산은 원리가 어렵다기보단

실수 없이 잘 해내는 것이 중요하다 보니 많은 연습을 통해 익숙해지는 것이 중요할 거예요.

여기까지!