■ 목표
- 수 체계의 확장
- 수 집합의 포함관계

수 체계의 확장
수 체계(Number System)는 우리가 배워온 모든 숫자들이
어떤 성질들을 가지는지, 어떤 연산이 가능한지 등을 연구한 것이에요.
그 과정에서 새로운 숫자를 발견하게 됩니다.
그 발견의 역사를 간단하게 살펴볼까요?
■ 자연수(Natural Number)
$1, 2, 3, …$ 등
우리가 가장 처음 알고 있던 수입니다.
귤이 3개 있는 걸 보고, $3$ 이라는 숫자를 떠올릴 수 있듯
실생활에서 가장 먼저 접할 수 있는 수입니다.
이제 자연수를 가지고 $+, -$ 을 해봅니다.
$2+x=3$ $∴ x=1$
$2+x=2$ $∴ x=2-2=?$
$2+x=1$ $∴ x=1-2=?$
바로 문제가 생기죠.
자연수는 뺄셈에서 자유롭지 않습니다.
즉, 자연수에서 자연수를 뺀 수가 자연수에는 없었습니다.
그래서 우리는 $0$, $-1$ 등의 수를 모두 포함한
정수라는 수 체계로 범위를 확장합니다.
■ 정수(Integer)
정수는 우리가 알고 있던 모든 자연수인 $n=1, 2, 3, …$
그 자연수에 $-$ 를 붙인 $-n=-1, -2, -3, …$
그리고 $0$ 으로 구성되어 있습니다.

이제 정수는 $+, -$ 에 대해 자유롭습니다.
하지만, $\times, \div$ 에 대해서는 그렇지 않았죠.
$2\times x=4$ $∴ x=2$
$2\times x=2$ $∴ x=1$
$2\times x=1$ $∴ x=1\div2=?$
$1$ 이라는 수가 반으로 나눠진다는 건 생각도 안 해봤습니다.
하지만, 분명 존재하는 수이죠.
이 수를 앞으로 $0.5$ 처럼 소수 혹은 $\frac{1}{2}$ 처럼 분수로 표현하기로 합니다.
이렇게 나누기가 가능한 모든 수를 포함해서
유리수로 확장합니다.
■ 유리수(Rational Number)
이제 모든 수는 분수꼴로 표현할 수 있습니다.
정수는 분모가 $1$ 인 분수($1=\frac{1}{1}$, $2=\frac{2}{1}$ 등)이고,
정수가 아니라면 분모가 $1$ 이 아닌 분수입니다.

드디어 유리수는 사칙연산으로부터 자유롭게 되었습니다.
즉, 유리수를 가지고 아무리 $+, -, \times, \div$ 해보아도
유리수만 나옵니다.
이젠 거듭제곱입니다.
같은 수를 두 번 곱하는 것뿐이니 별 문제가 없을 줄 알았습니다.
$x^2=4$ $∴ x=±2$
$x^2=2$ $∴ x=?$
같은 수를 두 번 곱해서 2가 되는 수.
솔직히 찾으려면 찾을 수는 있습니다. $x=±1.414213…$
하지만, 이 수의 소수 부분엔 규칙이 없어서 무한히 써야만 했죠.
그래서, 제곱근(Root)이라는 기호를 도입해서 $x=±\sqrt{2}$ 이렇게 표현하기로 합니다.
모든 분수인 유리수는 소수로 나타내었을 때,
유한소수이거나 순환하는 무한소수 즉, 순환소수가 됩니다.
하지만, "순환하지 않는 무한소수" 들은 분수꼴로 나타내지 못합니다.
즉, 이 수들을 "무리수(Irrational Number)" 라고 하고,
이를 포함해서 실수로 확장합니다.
■ 실수(Real Number)
이제 이 세상에 존재하는 모든 수를 거의 다 찾아냈다고 할 만합니다.
우리는 수의 대소관계를 비교하기 위해 수직선을 활용하는데,

정수와 정수 사이의 많은 빈 공간에

수도 없이 많은 유리수와 무리수가 꽉 채워지면서
수직선을 빈틈없이 메울 수 있었기 때문이죠.
하지만, 해결하지 못한 한 가지 문제가 남아있었습니다.

과연 제곱해서 $-1$ 이 되는 숫자는 존재하는가?
사실 이것만큼은 누구도 건드리고 싶지 않았습니다.
$(-1) \times (-1)=1$ 이 되는 것처럼
음수를 두 개 곱하면 양수가 되는 게 당연했기 때문이죠.
하지만, 방정식을 풀 때마다 계속해서 등장하는 이런
"제곱해서 음수가 되는 수" 들을 "허수(Imaginary Number)" 라는 이름으로
결국은 받아들이기로 합니다.
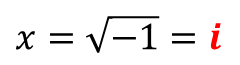
가장 기본이 되는 허수인 $\sqrt{-1}$ 을
"$i$" 라는 기호로 표현하고, "허수단위" 라고 부릅니다.
이를 이용하면,
$\sqrt{-4}=\sqrt{4} \times \sqrt{-1}=2i$
$\sqrt{-5}=\sqrt{5} \times \sqrt{-1}=\sqrt{5}i$
이렇게 모든 허수를 "$i$" 로 표현할 수 있죠.
이 허수를 포함해서 수는 복소수로 확장됩니다.
그리고 드디어 복소수에서는 문제없이 모든 계산이 가능하기 때문에
더 이상의 확장 없이 마무리가 됩니다.
수 집합의 포함관계
집합이란 용어는 원래 고1-2학기 과정인 수(하)에서 제대로 배우겠지만,
간단히 "모든 숫자들을 모아놓은 그룹" 이라고 생각하면 됩니다.
보통 집합들은 영어 대문자인 A, B 등으로 표현하는데,
수의 집합들은 특별히 정해진 고유문자로 표현합니다.
자연수를 모두 모아놓은 집합은
Natural Number 의 N으로 표현합니다.
정수는 영어로는 Integer 이지만 혼동을 피하기 위해,
독일어인 Zahlen 에서 따온 Z를 사용합니다.
유리수도 영어로는 Rational Number 이지만,
나눗셈에서 등장하는 몫(Quotient) 에서 따온 Q를 사용합니다.
그리고
실수는 Real Number 의 R
복소수는 Complex Number 의 C
이렇게 표현합니다.
지금까지 배운 수들의 포함관계를 살펴보면
다음과 같습니다.

"어떤 수 집합이 어떤 수 집합 안에 포함되는지" 를
더 쉽게 보는 방법은 그림으로 그려보는 것이죠.

예를 들어,
$0$ 의 경우, 정수이고 유리수, 실수, 복소수이다 모두 맞는 말이지만,
자연수이다는 틀린 말이죠.
자연수의 집합에 포함되지는 않는 수이니까요.
마무리
여기까지 허수를 발견하고
복소수까지 확장하게 된 배경을 살펴봤어요.
다음엔 본격적으로 복소수의 성질에 대한 얘기를 해볼게요!
'공통수학1 [고1] > 4. 복소수' 카테고리의 다른 글
| 조건을 만족하는 복소수 찾기 (0) | 2023.05.01 |
|---|---|
| 음수의 제곱근 (0) | 2023.04.23 |
| 켤레복소수의 정의와 성질 (2) | 2023.04.16 |
| 복소수의 사칙연산과 거듭제곱 (0) | 2023.04.08 |
| 복소수(Complex Number) (0) | 2023.04.02 |





댓글