■ 목표
- 복소수의 정의
- 두 복소수가 같을 조건

복소수(Complex Number)
지난번에 $x^2=-1$ 이라는 방정식의 해를
다음과 같이 정의하기로 했습니다.

이 $i$ 라는 기호를 허수단위라고 하고,
제곱해서 음수가 되는 모든 수들을
앞으로는 이 단위를 이용해서 나타내기로 합니다.

이렇게 말이죠.
새로운 기호가 도입이 되면
기존의 수들과 더해지지는 않아요.
루트($\sqrt{ }$) 가 도입되었을 때도,
$1+\sqrt{2}$ 는 그냥 그 자체로 하나의 수라고 봤죠.
마찬가지로, $1+i$ 도 그냥 하나의 수입니다.
분명, 하나의 수인데 그 안에는
실수인 부분도 허수인 부분도 있습니다.
그래서 "복합적인 두가지 요소를 가진 수" 라는 의미로
이름을 복소수라고 합니다.
■ 복소수의 구조
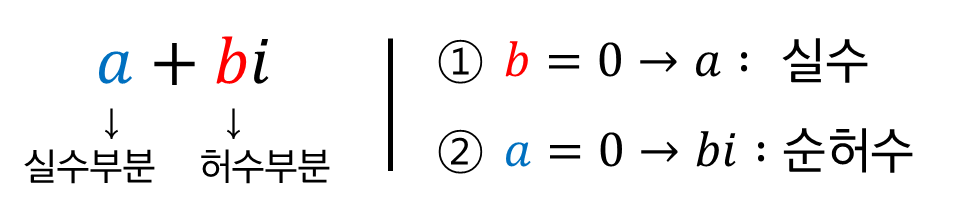
예를 들어, $2-3i$ 라는 복소수가 있다고 하면,
실수부분은 $2$, 허수부분은 $-3$ 이 됩니다.
(※ 허수부분을 $-3i$ 라고 하면 안됩니다!)
또, 이 수는 $i$ 라는 허수단위가 있으니 허수이고,
$-3i$ 처럼 실수부분이 없는 수는 순허수라고 합니다.
두 복소수가 같을 조건
보통 미지수를 나타낼 때, $x$ 나 $y$ 를 많이 사용하는데,
복소수에서는 $z$ 를 사용해서 조금 차별화를 둡니다.
자 그럼 여기 두 개의 복소수가 있습니다.

"두 복소수가 같다" 는 말은 무슨 말일까요?
두 복소수 모두 실수부분과 허수부분이 있으므로,
두 복소수가 같다는 건, 실수부분도 같고, 허수부분도 같다는 뜻입니다.

어떤 복소수가 실수 혹은 순허수인 경우에 조금 헷갈려하기도 하는데요,
그냥 $a$ 나 $b$ 중 하나가 $0$ 이라고 생각하면 괜찮을 거예요.
■ 예제
Q. 다음 식을 만족시키는 실수 $a$, $b$ 의 값을 구하시오.
(1) $a+bi=4i$
(2) $a+bi=-3$
(3) $a+bi=2i-\sqrt{3}$
(4) $(a-1)+(2+b)i=3-i$
(정답)
(1) $a=0$, $b=4$
(2) $a=-3$, $b=0$
(3) $a=-\sqrt(3)$, $b=2$
(4) $a=4$, $b=-3$
마무리
여기까지
복소수의 정의와 기본적인 구조를 살펴보았어요.
다음엔 복소수의 계산을 해볼게요.
'공통수학1 [고1] > 4. 복소수' 카테고리의 다른 글
| 조건을 만족하는 복소수 찾기 (0) | 2023.05.01 |
|---|---|
| 음수의 제곱근 (0) | 2023.04.23 |
| 켤레복소수의 정의와 성질 (2) | 2023.04.16 |
| 복소수의 사칙연산과 거듭제곱 (0) | 2023.04.08 |
| 수 체계의 확장 (0) | 2023.03.27 |





댓글