인수분해 방법(4/4) - 인수정리/조립제법

■ 목표

- ① 인수정리로 인수 찾기

- ② 조립제법으로 인수분해하기

 

 

 

 

 

①인수정리로 인수 찾기

 

인수정리란 한마디로

"어떤 식으로 나누어 떨어졌다" 면 그건 "인수" 다.

이를 이용해서 근을 찾을 수 있었죠.

 

 

예를 들어,

$f(x)$ 가  $(x-2)$ 로 나누어 떨어졌다면,

$f(2)=0$ 이라는 걸 알 수 있습니다.

 

 

<참고> 인수정리

인수정리

 

 

인수분해 단원에서는 반대로

근을 이용해 인수를 찾는 것이 목적입니다.

 

 

그래서 조금 까다롭지만,

$f(α)=0$ 이 되는  $α$ 를 먼저 찾아서,

$(x-α)$ 가 인수라는 것을 알아내는 것이죠.

 

---

■ 예시

 

 

이 식의 인수를 찾으려면 먼저 근을 찾아야 합니다.

즉,  $x$ 에 어떤 값을 대입해야  $0$ 이 되는 지를

추리하는 것이죠.

 

 

 

 

만약, 이렇게 3개의 근을 찾아냈다면,

성공적으로 3개의 인수를 찾아낸 것이죠.

따라서, 이렇게 인수분해가 됩니다.

 

 

 

 

하지만, 문제는

"근을 도대체 어떻게 찾느냐" 겠죠.

 

---

 

하나하나 대입하면서 계산해봐야 하는 것도 맞지만,

그래도 몇 개의 후보를 쉽게 추려내는 건 가능합니다.

 

 

 

 

결국 인수로 밝혀진

$(x-1)$,  $(x+1)$,  $(x-2)$ 에서 중요한 건,

상수항들입니다.

이 상수항  $-1$, $1$, $-2$ 를 전부 곱한 항은

원래식의 상수항인  $2$ 와 같습니다.

 

 

이 사실을 잘 생각해 본다면, 답은

상수항  $2$ 의 약수인  $1$,  $-1$,  $2$,  $-2$

중에 있다는 걸 알 수 있죠.

 

---

 

하지만, 정말 찾기 어려운 경우도 있습니다.

 

 

 

 

우리가 근을 찾을 수 있는 유일한 인수는  $2x-1$.

즉,  $x=\frac{1}{2}$ 인 경우입니다.

 

 

 

 

$2x-1$ 이 나온 이유는

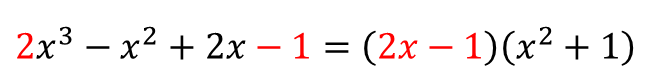
최고차항의 계수가  $2$ 이기 때문에 그렇습니다.

 

 

따라서, 근의 후보는

상수항의 약수인  $1$,  $-1$  뿐 아니라

최고차항의 약수중  $2$ 로 나눈

$\frac{1}{2}$,  $-\frac{1}{2}$ 까지입니다.

 

 

정리하면 다음과 같습니다.

 

■  $f(x)$ 의 인수  $(x-α)$ 의 후보 찾기

 

​

 

②조립제법으로 인수분해하기

 

아무리 그래도

근을 3개씩이나 찾는 건 너무 힘듭니다.

 

 

그래서 우리는 근을 딱 하나만 찾은 후에

그냥 나눗셈을 해버리는 방법으로 인수분해합니다.

 

 

바로 조립제법을 사용하는 것이죠.

 

---

■ 예시

 

 

$x=1$ 을 대입하면  $f(1)=0$ 이 된다는 사실은

꽤 쉽게 찾아낼 수 있습니다.

그다음 바로 조립제법으로 나눗셈을 합니다.

 

 

 

 

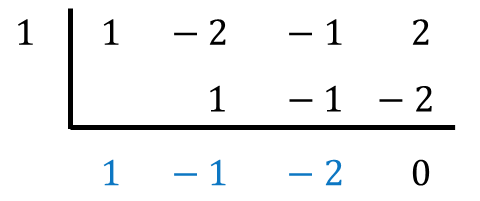
그럼 몫을 구할 수 있고,

2차식 정도는 간단하게 인수분해할 수 있게 되죠.

 

 

 

---

 

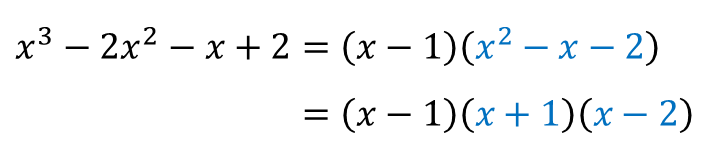
인수정리와 조립제법을 이용한 인수분해 방법을

최종정리하면 다음과 같습니다.

 

 

■ $f(x)$ 인수분해하기

① 인수정리 : 근 α 찾기 → 인수  $(x-α)$ 찾기

 

 ② 조립제법 : $f(x)$ 를  $(x-α)$로 나누기

 

 

 

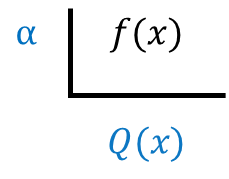
마무리

 

이 인수분해 방법은 꽤 많이 사용됩니다.

앞으로 다루게 될 3차, 4차 방정식의 풀이를 위해서죠.

 

 

특히, 3차 다항식은 이 방법으로

100% 인수분해가 가능하니 꼭 알아두어야 해요.