■ 목표
- 실수범위 계수의 인수분해란
- A. 두 일차식의 곱으로 인수분해하기
- B. 인수분해되도록 하는 상수 k값 찾기

개요
수(상)에서 심화 문제로 가끔 등장하는
유형 한 가지를 살펴보고자 해요.
■ 예시
다음 식이 $x$, $y$ 에 대한 두 일차식의 곱으로 인수분해될 때,
상수 $k$ 의 값을 구하시오.
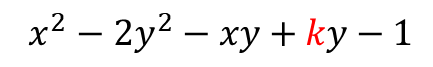
일단 인수분해할 방법이 마땅히 떠오르지 않아서
많이들 당황하는 유형입니다.
우선, 억지로(?) 인수분해하는 방법을 배워서
A. 실제로 인수분해를 해보고
B. 인수분해 되도록 하는 상수 $k$ 를 구해보는
순서로 차근차근 살펴볼게요!
실수범위 계수의 인수분해란
인수분해는 일반적으로
계수가 유리수인 범위 내에서만 합니다.

그래서 이런 식은
"인수분해가 되지 않는다" 고 하죠.
하지만, 계수의 범위를 실수까지 확장한다면 가능합니다.
근을 구할 수만 있다면 말이죠.
어떤 이차식의 두 근이 $α, β$ 라고 하면,
다음과 같이 인수분해할 수 있습니다.

$x^2-2x-2=0$ 의 근을 구해보면
$x=1+\sqrt{3}$, $x=1-\sqrt{3}$ 이죠.
즉, 이렇게 인수분해 가능합니다.

복잡해보여서 잘 안 쓰일 것 같지만
어떻게든 근을 구할 수만 있다면,
확실히 인수분해 가능하다는 건 알 수 있습니다.
A. 두 일차식의 곱으로 인수분해하기
다시 원래 문제로 돌아와 볼게요.
■ 예시
다음 식이 $x$, $y$ 에 대한 두 일차식의 곱으로 인수분해될 때,
$k$ 의 값을 구하시오.
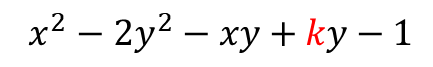
이제 실제로 인수분해를 해볼 텐데,
대충 때려 맞춰 추리하는 방법도 있긴 합니다.
"$x$, $y$ 에 대한 두 일차식의 곱" 이라 했으니,
분명 아래와 같은 모양으로 인수분해되겠죠.

여기서 모르는 6개의 계수를 전부 추리하는 것입니다.
왠지 $a=1$, $d=1$ 일 것 같고...
하다 보면 딱 맞아떨어지기도 하죠.
하지만, $a \times d=1$ 이라는 게
무조건 $a=1$, $d=1$ 임을 의미하는 건 아니다 보니
생각보다 찾기가 어려운 경우도 많습니다.
그래서 조금 어려울 수 있지만
확실한 방법으로 해볼게요.
■ 두 일차식의 곱으로 인수분해하기
① 한 문자를 기준으로 내림차순 정리하기
② 이차방정식의 근 구하기
③ 두 근을 이용해서 인수분해하기
① 한 문자를 기준으로 내림차순 정리하기

$x$ 를 기준으로 내림차순 정리하면
$x$ 에 대한 이차식이 됩니다.
② 이차방정식의 근 구하기
여기가 조금 힘듭니다.
근을 구하기 위해서는 근의 공식을 쓸 수밖에 없죠.

ㅗㅜㅑ...
근을 구해보니 생긴 게 굉장합니다.
암튼 두 근은 "$y$ 에 대한 식" 이기 때문에
쉽게 두 근을 $x=Y_1, Y_2$ 라고 쓰도록 하겠습니다.
③ 두 근을 이용해서 인수분해하기
그러면 두 근인 $Y_1, Y_2$ 를 이용해서 다음과 같이 인수분해 됩니다.

B. 상수 $k$ 구하기
인수분해는 어떻게든 할 수 있지만 중요한 건,
"$x$, $y$ 에 대한 두 일차식의 곱" 으로 인수분해된다는 점입니다.

즉, 여기서 $Y_1$, $Y_2$는 모두 "$y$ 에 대한 일차식" 이어야만 합니다.
이걸 이용해서 $k$ 를 구할 수 있습니다.

이게 일차식이어야 하죠.
그 말은 "루트 안에 있는 식"

이 식이 반드시 완전제곱식이어야 한다는 뜻입니다.
그래야 루트가 사라지고 일차식이 될 테니까요.
즉, "루트 안에 있는 식" 의 판별식은 $0$ 이어야 한다.
$4k^2-36=0$ 이므로
$k=3$ 또는 $k=-3$ 입니다.
■ 검산
① $k=3$ 이라면,
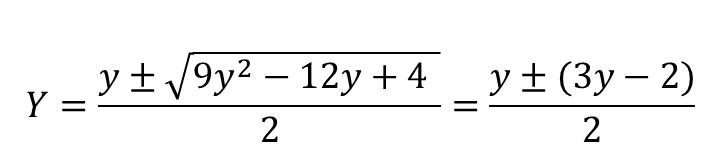
즉, $Y_1=-y+1$, $Y_2=2y-1$ 입니다.
그래서 이렇게 인수분해됩니다.
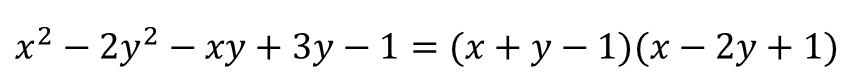
② $k=-3$ 이라면,

즉, $Y_1=-y-1$, $Y_2=2y+1$ 입니다.
그래서 이렇게 인수분해됩니다.

굉장히 길고 힘든 과정이었네요.
어쨌든 구하고자 하는 건 $k$ 이니,
$k$ 를 구하는 과정만 요약을 해서 살펴볼까요.
■ 두 이차식으로 인수분해될 때, 상수 $k$ 구하기
① $x$에 대해 내림차순 정리하기
② 판별식이 완전제곱식(★)
③ 판별식의 판별식이 $0$
■ 예제
다음 식이 $x$, $y$ 에 대한 두 일차식의 곱으로 인수분해될 때,
$k$ 의 값을 구하시오.
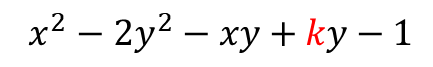
(풀이)
① $x$에 대해 내림차순 정리하기
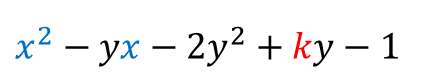
② 판별식이 완전제곱식(★)
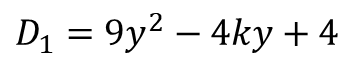
③ 판별식의 판별식이 0
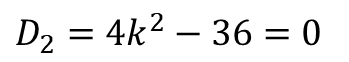
그러므로, $k=3$ 또는 $k=-3$.
마무리
심화유형인 이유가 있죠?
단순히 인수분해 방법을 외우는 것이 아니라
내림차순 정리나 인수분해에 대한 깊은 이해를
하고 있는지 확인하고자 하는 유형이에요.
어렵겠지만 차근차근해보면서 자기 것으로 만들어보면 좋겠어요!
'공통수학1 [고1] > 3. 인수분해' 카테고리의 다른 글
| 문자가 여러 개인 다항식[심화2](1/4) - 다변수 다항식의 구분 (1) | 2023.03.12 |
|---|---|
| 인수분해 방법(4/4) - 인수정리/조립제법 (0) | 2023.03.12 |
| 인수분해 방법(3/4) - 내림차순 정리 [문자가 여러 개인 다항식] (0) | 2022.12.27 |
| 인수분해 방법(2/4) - 치환 [B. 복이차식] (0) | 2022.12.14 |
| 인수분해 방법(2/4) - 치환 [A. 공통부분이 있는 유형] (0) | 2022.12.10 |





댓글