■ 목표
- 치환이란
- 공통부분이 있는 유형 인수분해 해보기

치환이란
치환은 "바꾸어 놔둔다"는 뜻입니다.
"바꿔치기" 같은 이미지로 생각하면 좋겠네요.
식을 전개하거나 인수분해할 때는
항이 많아서 복잡한 경우에 치환을 쓰게 되죠.

이런 식으로 말이죠.
"여러 개의 항" 또는 "식 자체"를
하나의 문자로 치환해서
복잡한 계산을 쉽게 할 수 있도록 해줍니다.
A. 공통부분이 있는 유형
다항식은 당연히
항이 많을수록 복잡해집니다.
그래서 치환을 이용해서 항을 줄이면
쉬운 인수분해가 가능해지는 유형이라고 볼 수 있습니다.
이때, 어떤 부분을 치환해야 할지를
잘 알아보는 것이 중요하겠죠?
우선은 그냥 대놓고 공통부분을 보여주는
쉬운 유형입니다.
■ 예시1

인수분해가 된 것 같아 보이지만
완전히 "곱으로만 표현"된 것이 아니네요.
그래서 이걸
① 전부 전개한 다음
② 다시 인수분해를 해야 합니다.
항이 6개나 나오는 전개는
생각만 해도 귀찮은데요.
이럴 때 치환을 쓰는 겁니다.
너무 똑같이 생긴 $x^2-x$ 를 말이죠.
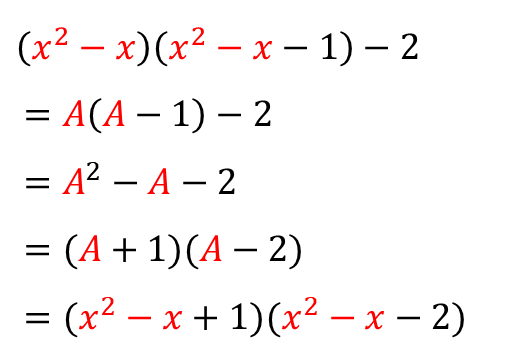
너무도 쉬운 인수분해 문제가 되어버리죠.
하지만, 이건 너무 쉬운 것 같으니
공통부분이 안 보이도록 숨겨놓는 유형도 있습니다.
■ 예시2

마땅히 치환할 만한 부분이 안보이죠?
그렇다고 저걸 다 전개할 순 없으니
우선은 두 개씩만 전개를 해볼 건데요
어떤 두 식을 전개하면 좋을까요?
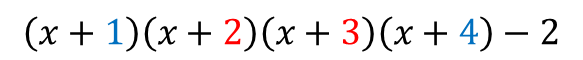
전개했을 때의 결과를 생각해봐야 해요
$1+4$ 와 $2+3$ 이 같다는 건
전개했을 때, $x$ 항의 계수가 $5$ 로 같다는 거예요.
즉, 전개를 하면 공통부분이 생깁니다.

비슷한 문제를 몇 번 풀다보면
많이 어렵지는 않은 유형일 거예요.
마무리
여기까지!
치환을 사용하는 가장 기본적인 유형이었어요.
다음은 "복이차식" 을 치환을 이용해서
인수분해 해볼게요!
'공통수학1 [고1] > 3. 인수분해' 카테고리의 다른 글
| 문자가 여러 개인 다항식 [심화1] - 인수분해되도록 하는 계수 찾기 (0) | 2022.12.30 |
|---|---|
| 인수분해 방법(3/4) - 내림차순 정리 [문자가 여러 개인 다항식] (0) | 2022.12.27 |
| 인수분해 방법(2/4) - 치환 [B. 복이차식] (0) | 2022.12.14 |
| 인수분해 방법(1/4) - 인수분해 공식 (0) | 2022.11.28 |
| 인수분해 개요 (0) | 2022.11.24 |





댓글