조립제법

■ 목표

- 조립제법 사용 조건 알기

- 조립제법으로 몫과 나머지 구해보기

 

 

 

 

조립제법 사용 조건

 

조립제법으로 직접 나눗셈을 해볼까해요.

$3x^3-8x-2$ 를  $2x+2$ 으로 나누어 볼게요.

 

문제를 이렇게 표현할 수 있겠죠.

 

 

근데, 조립제법을 쓰기 전에는

꼭 지켜야 할 두 가지 중요한 조건이 있습니다.

 

① 명확한 자릿수의 표시

자릿수라는 표현이 이상할 수도 있지만, 비슷한 맥락이긴 합니다.

 

우리는 편의상 문자를 쓰지 않고, 계수만 쓰기로 했죠.

이때, 계수는 내림차순으로 적습니다.

하지만 보이는 대로만 쓰면 문제가 생깁니다.

 

 

오른쪽 배열을 보면  원래 식이  $3x^2-8x-2$ 인 것처럼 보이겠죠.

따라서 보이지 않는  $x^2$ 항까지 꼭 써야만,

$3$ 이  $x^3$ 의 계수라는 것을 알 수 있습니다.

 

 

마치,  백의 자리수가  $0$ 이라고 생략했다간

$3082$ 가 아니라  $382$ 가 되어버리는 것과 같은 맥락이죠.

 

②  $(x+α)$ 꼴의 식으로만 나눌 수 있다

즉,  $(2x+2)$ 로는 조립제법을 쓸 수 없습니다(!!)

많은 계산과정이 생략될 수 있었던 이유도

최고자항의 계수가  $1$ 이었기 때문입니다.

 

하지만, 생각보다 간단한 트릭을 이용하면 조립제법이 가능해집니다.

바로  $x$ 에 곱해진  $2$ 를

몫인  $Q(x)$ 에 넘겨주는 것이죠.

 

 

그럼 이제 문제없으니, 조립제법을 해볼까요.

 

 

■ 조립제법 사용

 

 

계산 결과로  $2Q(x)$ 와  $R(x)$ 를 찾았습니다.

정리하면

 

 

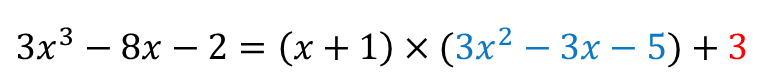
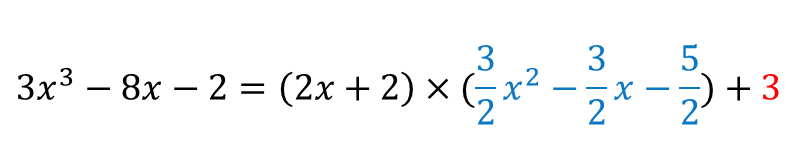
이렇게 되겠죠.

몫의 계수들이 분수라서 더럽(The love..)지만

다항식의 나눗셈을 성공적으로 해냈습니다.

 

우리가 식을 전부 외우지 않은 이상

조립제법은 몫과 나머지를 구하는 가장 빠른 방법입니다.

다만, 모든 나눗셈 문제에서 사용할 수는 없을 뿐이죠.

 

조립제법을 사용할 수 있는 조건은

 

 

나누는 식  $B(x)$ 가  $(x+α)$ 일 때 만입니다.

혹은 억지로 만들 수 있다면 역시 가능하죠.

 

 

 

마무리

 

여기까지!

첫번째 대단원은 여기서 끝이예요.

다음 단원부터는 본격적으로

식의 나눗셈을 주로 다루게 됩니다.

2단원에서 뵈요!