■ 목표
- 행렬의 연산의 성질
- A. 교환법칙
- B. 결합법칙
- C. 분배법칙

개요
새 연산을 배울 때 항상 확인해야 하는 것,
바로 연산의 성질입니다.
복잡한 계산을 할 때, '어디까지 허용되는지'를
확인하는 과정이라고 보면 되죠.🔍
연산의 성질엔 세 가지
교환법칙, 결합법칙, 분배법칙이 있습니다.
그럼 '행렬의 연산'의 성질은 어떨까요?
A. 교환법칙⭐
교환법칙이란 한 마디로
'연산기호의 앞, 뒤 숫자가 교환되어도 결과가 같은가' 입니다.
덧셈과 곱셈은 교환법칙이 성립하죠.
$2+3=3+2$
$2 \times 3 = 3 \times 2$
행렬의 덧셈은 어떨까요?
행렬에서 덧셈은
각 성분끼리의 덧셈들로 이루어집니다.

일반적인 덧셈을
네 번하는 것뿐이기 때문에
당연히 교환법칙은 성립합니다.
즉, $A+B=B+A$ 로 표현할 수 있습니다.
하지만, 행렬의 곱셈은 어떨까요?🤔
행렬의 곱셈방법을 생각해 보면
일반적인 곱셈과는 확실히 다르죠.

따라서, 두 행렬을 곱하더라도
앞의 행렬과 뒤의 행렬의 위치가 바뀌면,
결과도 달라집니다!
즉, 행렬의 곱셈은
교환법칙이 성립하지 않습니다.🥺
$A \times B \neq B \times A$
B. 결합법칙
결합법칙이란 한 마디로
'연산기호를 여러 번 사용할 때, 순서에 상관없이 결과가 같은가' 입니다.
예를 들어,
$2+3+5$ 같은 계산을 할 경우,
$2+3$ 을 먼저 하든, $3+5$ 를 먼저 하든
결과는 같습니다.
$(2+3)+5=5+5=10$
$2+(3+5)=2+8=10$
행렬의 덧셈과 곱셈은
모두 결합법칙이 성립합니다.
$(A+B)+C=A+(B+C)$
$(A \times B) \times C=A \times (B \times C)$
※ 과정이 복잡해서 증명은 보통 생략하지만😵
$2 \times 2$ 행렬의 곱셈에서 하나의 성분만 살펴보자면
아래와 같습니다.
$(A \times B) \times C$
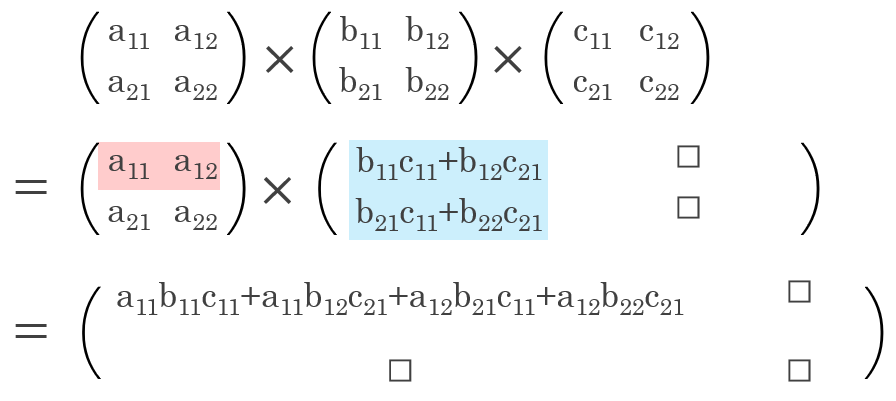
$A \times (B \times C)$

C. 분배법칙
마지막인 분배법칙은
덧셈과 곱셈의 혼합계산입니다.
$a \times (b+c) = ab+ac$
$ab+ac = a \times (b+c)$
행렬에서도 분배법칙은 성립합니다.
$A \times (B+C) = AB+AC$
$AB+AC = A \times (B+C)$
※ 역시 과정이 복잡해서 증명은 생략하지만,
간단히 살펴보자면 아래와 같습니다.
$A \times (B+C)$
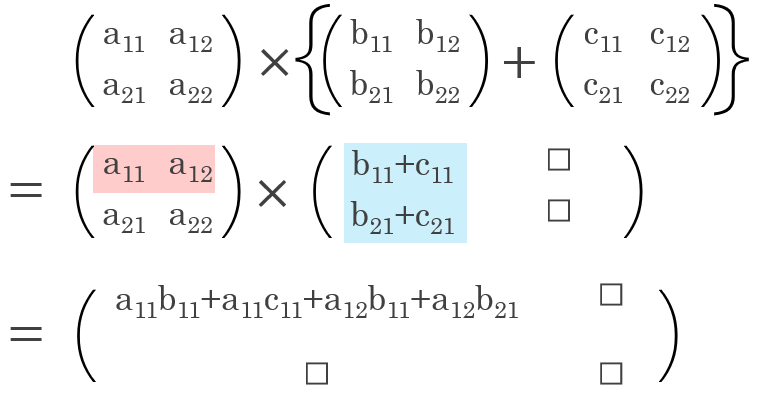
$AB+AC$
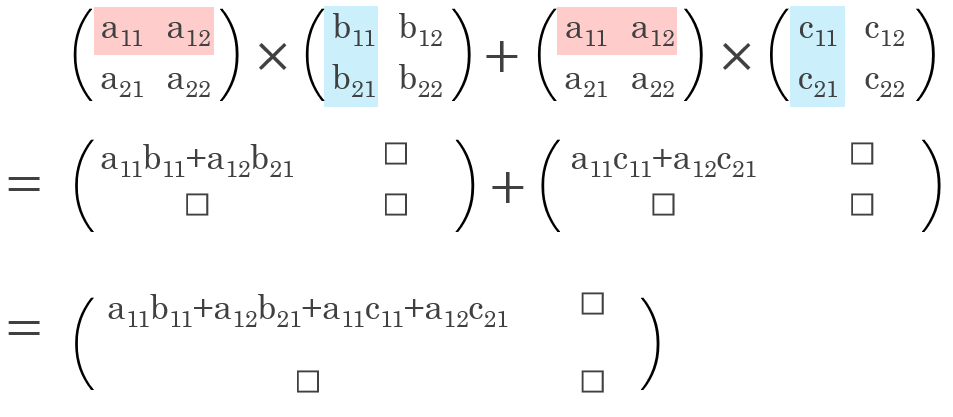
마무리
이제 결론입니다.
행렬의 덧셈과 곱셈은 자유롭게 계산가능합니다.
단, 행렬의 곱셈만 빼고!
$A \times B \neq B \times A$
딱 하나 성립하지 않는 곱셈의 교환법칙 때문에
많은 것들이 헷갈리기 시작하고,
이 단원은 그걸 노려서 문제로 낸답니다😒
'공통수학1 [고1] > 11. 행렬' 카테고리의 다른 글
| 항등원과 행렬의 연산 (0) | 2024.04.21 |
|---|---|
| 행렬의 연산2 - 곱셈 (0) | 2024.04.14 |
| 행렬의 연산1 - 덧셈, 뺄셈, 상수배 (0) | 2024.04.08 |
| 행렬이란? (0) | 2024.03.10 |





댓글