■ 목표
- 행렬의 뜻 알기
- 행렬의 성분 알아보기
- 정사각행렬의 뜻 알기
- 행렬 만들어보기

개요
행렬은 2022년 개정 교육과정에서
오랜만에 다시 추가된 개념입니다.
요즘 개발이나 AI에 대한 관심이 많아지면서
다시 필요성이 커지고 있죠.
왜냐면, 행렬은 방대한 자료를 동시에 다루거나,
여러 자료들의 변환을 하기에 딱 좋은 훌륭한 도구거든요.📋
물론, 고등과정에서는 아주 기본적인 내용만 다루겠지만,
조금 깊게 배우고 나면, '연립방정식의 풀이'나 '벡터나 좌표의 변환' 등
수학 안에서도 활용할 수 있는 방안이 많답니다.
행렬이란?
행렬(Matrix)의 개념은
사실 우리에게 친숙한 '표'입니다!😲
가로줄을 행이라 하고, 세로줄을 열이라 하기 때문에
표는 행렬이라 하죠.(참 단순..)
우리는 많은 양의 데이터를 정리하거나
내용을 구분 지을 때 표를 사용하곤 합니다.
가계부나 시간표 등 말이죠.

가로/세로 선으로 자료를 구분해 놓으면
한눈에 쏙 들어온다는 장점이 있죠.
하지만, 수학은 귀찮은 걸 정말 싫어합니다.
저 많은 선을 다 그리는 시간이 아깝죠.😒
수학에서는 표를 좀 더 간단하게 표시하기로 합니다.
그냥 '표'라는 표현만 해주고 나서,
숫자 사이사이에 간격만 잘 넣어주면 표처럼 보이거든요.💡
아래와 같이 말이죠.

이처럼 "같은 간격으로 나열된 숫자들을
거대한 괄호 ( )로 감싼 것" 을 수학에서의 표
즉, 행렬이라고 부릅니다.
행렬의 성분
행렬에서 중요한 건 당연히 그 안에 들어있는 내용들인데,
이를 행렬의 성분이라고 합니다.
이 하나하나의 성분들은 그 위치가 중요합니다.
저기 "9"라는 성분의 위치를 어떻게 설명해야 할까요?🤔

모든 사람이 헷갈리지 않고 설명하기 위해
방법을 정하기로 합니다.
가로줄, 세로줄의 순서대로 얘기하기로 말이죠.
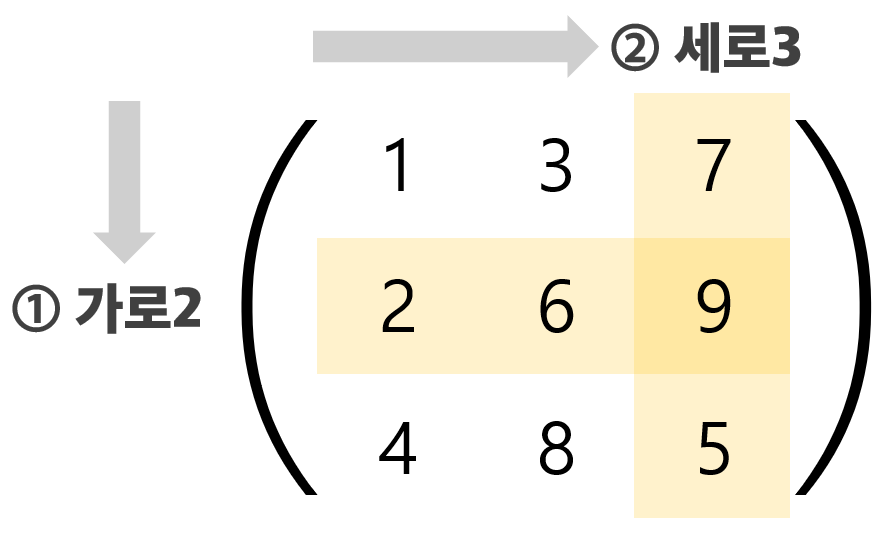
9는 "가로 2번째 줄, 세로 3번째 줄의 성분"입니다.
행과 열이라는 단어를 사용하면, 더 간단하죠.
9는 "2행 3열의 성분"입니다.
임의의 행렬을 문자로 놓을 때는
행렬은 알파벳 '대문자 A'로, 그 안의 성분들은 '소문자 a'로 씁니다.
굳이 반대로 쓸 이유가 없죠?
이때, 각 성분을 a, b, c 로 쓰기도 하지만,
보통은 a에 성분의 위치를 함께 써줍니다.
각 숫자의 의미는 1행 1열, 1행 2열이라는 뜻입니다.
그러면 어떤 임의의 행렬을 표현할 때,
다음과 같이 표현할 수 있게 됩니다.
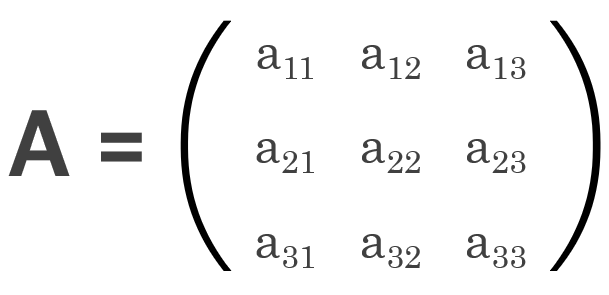
정사각행렬이란?
행렬의 사이즈는 "행 개수x열 개수" 로
다음과 같이 표현합니다.
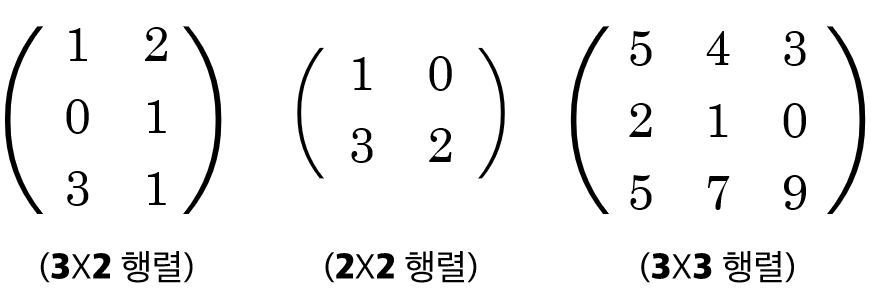
이 중에서 '행 개수'와 '열 개수'가 같은 행렬들은
특별히, 정사각행렬이라고 이름을 붙이는데요.
그만큼 깔끔하고, 자주 쓰이기 때문이죠.
간단하게
2x2 행렬은 2차 정사각행렬,
3x3 행렬은 3차 정사각행렬이라고 불러주면 됩니다.
지금껏 3차 정사각행렬을 썼기 때문에
성분도 9개나 되고, 복잡해 보였죠.😵
하지만, 걱정 마세요.
고등과정에서는 주로 2차 정사각행렬을 다룬답니다.👍
행렬 만들기
행렬에 익숙해지기 위해
한번 직접 만들어보는 연습을 해볼까요.
① 행렬의 사이즈: 2x2
가장 많이 활용되는 2차 정사각행렬입니다.
문자로 나타내면 다음과 같죠.
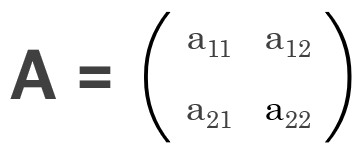
② 행렬의 성분 규칙
여기서 4개의 성분을 따로 적어도 되겠지만,
하나의 식을 주고, 직접 구해보도록 하는 문제도 있습니다.
규칙 :
...당황스럽죠?
갑자기 등장한
아직 정해지지 않은 행과 열을 말합니다.
즉, 이 규칙을 이용하면,
마찬가지로 모든 성분을 규칙을 통해 구할 수 있습니다.
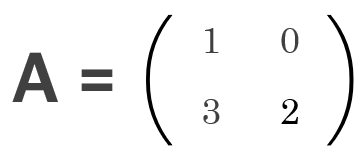
마무리
새로 배우는 것들 투성일 때는
많이 해보면서 익숙해지는 수 밖엔 없죠.
다행히 익숙해지기만 한다면
그 어떤 단원보다 쉬운 단원이 될 거예요.😎
'공통수학1 [고1] > 11. 행렬' 카테고리의 다른 글
| 행렬의 연산의 성질 (1) | 2024.06.06 |
|---|---|
| 항등원과 행렬의 연산 (0) | 2024.04.21 |
| 행렬의 연산2 - 곱셈 (1) | 2024.04.14 |
| 행렬의 연산1 - 덧셈, 뺄셈, 상수배 (0) | 2024.04.08 |





댓글