■ 목표
- 행렬의 곱셈원리 이해하기
- 곱셈이 가능한 조건 살펴보기

개요
행렬의 곱셈방법은 덧셈, 뺄셈과는 다르게
굉장히 독특합니다.✨
그냥 이렇게 계산하면 되지 않을까요?

라고 생각하면 절대 안 됩니다.😓
행렬의 곱셈원리는
어쩌면 행렬의 존재 이유와도 관련이 있습니다.
원래 연립방정식을 좀 더 빠르고 쉽게 풀고 싶어서 탄생한 게 행렬이거든요.
지금은 그 탄생배경이나 원리보다는
곱셈하는 방법만 우선 알아보도록 할게요.
행렬의 곱셈방법
가장 많이 사용되는 (2x2 행렬)의 곱셈에서
성분 하나씩 구하는 방법을 알아볼게요.
순서대로
앞행렬의 행과 뒷행렬의 열을 성분끼리 곱하면
새로운 성분 하나를 구할 수 있습니다.

(1행)과 (1열)을 곱해서 (1행 1열의 성분)을 계산한 모습입니다.
(1행) 첫 번째 성분인
(1행) 두 번째 성분인
더한 결과이죠.
마찬가지로 총 4번 계산을 진행하면
새로운 행렬의 4개 성분을 모두 구할 수 있습니다. 😵



■ 행렬의 곱셈방법

행렬의 곱셈 가능 조건
곱셈방법이 특이하다 보니
행렬끼리의 곱셈이 항상 가능한 건 아닙니다.
사이즈가 다른 행렬의 곱셈을 한번 살펴볼게요.

앞의 행에는 성분이 2개밖에 없는데
뒤의 열에는 성분이 3개입니다.
계산자체가 성립되지 않죠.😐
곱셈이 가능한 경우는 다음과 같습니다.
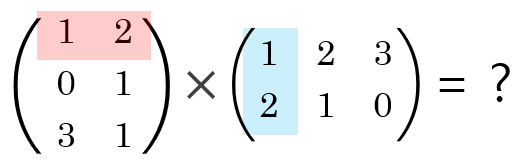
사이즈가 다른 행렬이더라도
앞행렬의 '행의 성분의 개수'와뒷행렬의 '열의 성분의 개수'가 같다면
곱셈이 가능합니다.
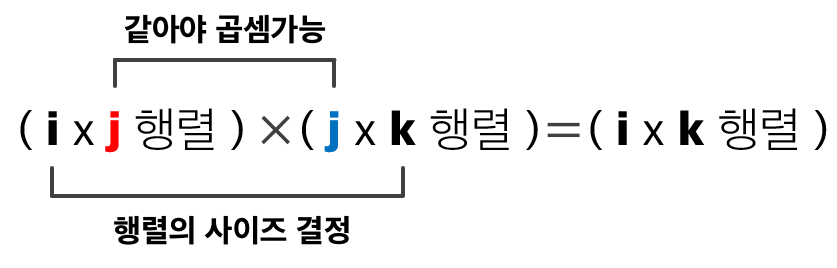
즉, 곱셈이 가능한 조건은
앞행렬의 '열 개수'와 뒷행렬의 '행 개수'가 같을 때입니다.💡

그리고 계산결과를 살펴보면
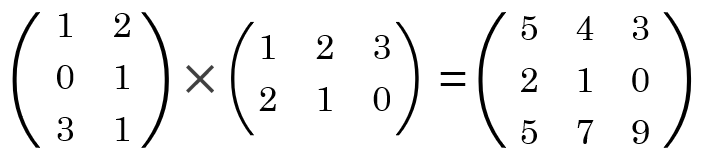
행 3개와 열 3개를 곱하면서
총 9번의 계산을 해야 하죠. 😵
결과는 3x3 행렬이 만들어집니다.

■ 행렬의 곱셈 가능 조건
마무리
곱셈은 몇 번만 연습해 보면
금방 익숙해지기 때문에
대부분의 문제들은 어렵지 않을 거예요.
하지만, 여전히
곱셈을 왜 이렇게 복잡하게 정의했는지에 대한
의문은 해결되지 않았죠.
이 얘기는 교과과정 외이기 때문에
기본 내용이 모두 끝난 후 심화로 포스팅할게요.😎
'공통수학1 [고1] > 11. 행렬' 카테고리의 다른 글
| 행렬의 연산의 성질 (0) | 2024.06.06 |
|---|---|
| 항등원과 행렬의 연산 (0) | 2024.04.21 |
| 행렬의 연산1 - 덧셈, 뺄셈, 상수배 (0) | 2024.04.08 |
| 행렬이란? (0) | 2024.03.10 |





댓글