■ 목표
- 대칭식이란
- 대칭식의 성질
- 대칭식의 기본정리

대칭식(Symmetric Polynomial)
대칭이란 무언가가 동등하다는 뜻입니다.
좌우대칭은 좌우의 모양이 같은 것이고,
선대칭은 어떤 선을 기준으로 양쪽이 같은 것이죠.
문자가 여러 개인 식 즉, 다변수 다항식에서는
각 문자의 역할이 완벽하게 동등한 식을
대칭식이라고 합니다.
그래서 $x$ 와 $y$ 의 "자리를 바꾸어도"
아무런 문제가 되지 않죠.
예를 들면,
$x+y+z$, $x^2+y^2+z^2$, $xy+yz+zx$, $3xyz$
이런 식들이 바로 대칭식입니다.
$x^2+y+z$, $2x+3y-z$
이런 식들은 대칭식이 아니죠.
대칭식인지 확인하는 방법은
실제로 문자 두 개를 골라서 서로 바꿔보면 됩니다.




만약, 바꿨는데도 원래 식과 완벽히 똑같은 식이 된다면
대칭식이라는 것을 알 수 있죠.
이 성질을 정리하면 다음과 같습니다.
■ 2변수 대칭식
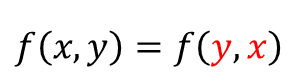
■ 3변수 대칭식
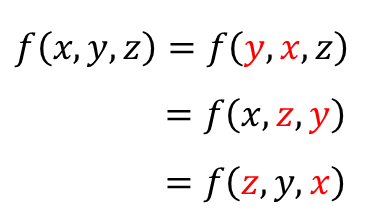
대칭식의 성질
대칭식이 가진 성질 중 쉬운 것 하나는
대칭식을 2개 가져와서 $+, -, \times, \div$ 해도
여전히 대칭식이 된다는 것입니다.
생각해 보면 당연한 말이기도 해요.
"$x$ 랑 $y$ 를 바꿔도 똑같아지는 식"을 두 개 더하면,
마찬가지로 "$x$ 랑 $y$ 를 바꿔도 똑같아지는 식" 이 됩니다.
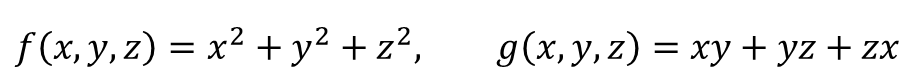

이렇게 말이죠.
■ 대칭식의 성질

대칭식의 기본정리

정리라는 건, 이미 정확한 증명을 거쳐서 검증된 말이에요.
그러니, 대칭식의 기본정리도 잘 이해하고 활용할 수만 있다면,
많은 대칭식 문제들을 편하게 풀어낼 수 있을 거예요.
우선은 기본대칭식이 뭔지 알아야겠군요.
기본대칭식은 가장 단순하게 만든 대칭식인데,
계수 없이 딱, 주어진 문자들만 가지고 만든 항들을 더하면 됩니다.
만약, $x$ 와 $y$ 라는 두 개의 문자로 기본대칭식을 만든다면,
$x$ 와 $y$ 를 하나만 딱 뽑아서 더한 $x+y$
$x$ 와 $y$ 를 같이 뽑아서 곱한 $xy$
이렇게 두 개만 기본대칭식이 됩니다.
차수에 따라
$x+y$ 는 1차 기본대칭식
$xy$ 는 2차 기본대칭식입니다.
그렇다면, 대칭식의 기본정리에 따라서
$x$ 와 $y$ 로 만든 모든 대칭식은
기본대칭식인 $x+y$ 와 $xy$ 로 이루어져 있다!
한번, 확인해 보죠.
■ 예시1
$x^2+y^2$ 은 2차 대칭식입니다.
따라서, 1차 기본대칭식을 두 번 곱한 $(x+y)^2$ 와
2차 기본대칭식인 $xy$ 를 몇 개씩 더하면 만들 수 있습니다.

기본대칭식을 몇 개 썼는가.
즉, 계수인 $a=1$ 와 $b=-2$ 는
식을 잘 비교해서 찾아내면 됩니다.
■ 예시2
$x^3+y^3$ 은 3차 대칭식입니다.
1차 기본대칭식을 세 번 곱한 $(x+y)^3$,
1차와 2차 기본대칭식을 곱한 $(x+y)xy$.
이거 말고는 3차를 만들 수 없겠군요.

사실 우리가 이미 외운 곱셈공식의 변형공식인데 새롭게 보이죠?
이번엔 3변수 다항식을 살펴볼게요.
■ 3변수 다항식의 기본대칭식
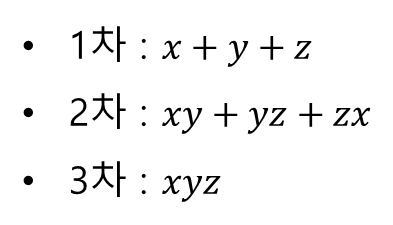
■ 예시3
$x^2+y^2+z^2$ 은 2차 대칭식입니다.
1차 기본대칭식을 두 번 곱한 $(x+y+z)^2$,
2차 기본대칭식인 $xy+yz+zx$ 로 만들 수 있습니다.

■ 예시4
$x^3+y^3+z^3$ 은 3차 대칭식입니다.
1차 기본대칭식을 세 번 곱한 $(x+y+z)^3$,
1차와 2차 기본대칭식을 곱한 $(x+y+z)(xy+yz+zx)$,
3차 기본대칭식인 $xyz$ 로 만들 수 있습니다.

여기선, 계수인 $a$, $b$, $c$ 찾는 게 어려울 수 있는데,
항을 하나씩 뽑아서 비교하는 방법으로 할 수 있습니다.
(계수 찾기)
왼쪽을 보면 $x^3$ 이란 항의 계수는 1이죠.
오른쪽에서 $x^3$ 을 만들려면 $a(x+y+z)^3$ 여기서 만들 수밖에 없으니 $a=1$ 입니다.
이번엔 $x^2y$ 항은 왼쪽에서 없으니 계수가 0입니다.
오른쪽에서는 $(x+y+z)^3$ 에서 $3x^2 y$, $b(x+y+z)(xy+yz+zx)$ 에서 $b3x^2 y$.
따라서, $b=-3$ 입니다.
마지막으로, $xyz$ 항의 계수는 0입니다.
$(x+y+z)^3$ 에서 $6xyz$,
$-3(x+y+z)(xy+yz+zx)$ 에서 $-9xyz$
따라서, $cxyz$ 에서는 $c=3$ 이어야 합니다.

묶어주고 정리하면,
우리가 아는 곱셈공식이 완성됩니다.
마무리
다변수 다항식 중 특이한 성질을 지닌 첫 번째인
대칭식에 대해 알아봤습니다.
대칭식의 기본정리를 통해서
식을 다른 모양으로 바꾸는 것도 해봤는데요.
우리의 최종목표는 사실 "인수분해 쉽게 하기" 입니다.
하지만, 그 방법을 배우기 위해 필요한 것이 많다 보니
긴 여정이 되고 있죠.
곧 마무리될 거예요!
다음 시간에는 교대식에 대해 배워볼게요.
'공통수학1 [고1] > 3. 인수분해' 카테고리의 다른 글
| 문자가 여러 개인 다항식[심화2](4/4) - 대칭식과 교대식의 인수분해 (0) | 2023.03.22 |
|---|---|
| 문자가 여러 개인 다항식[심화2](3/4) - 교대식(Alternating Polynomial) (0) | 2023.03.19 |
| 문자가 여러 개인 다항식[심화2](1/4) - 다변수 다항식의 구분 (1) | 2023.03.12 |
| 인수분해 방법(4/4) - 인수정리/조립제법 (0) | 2023.03.12 |
| 문자가 여러 개인 다항식 [심화1] - 인수분해되도록 하는 계수 찾기 (0) | 2022.12.30 |





댓글