■ 목표
- 3차 교대식/대칭식의 인수분해
- 4차 교대식/대칭식의 인수분해

3차 교대식/대칭식의 인수분해
먼저 인수분해 해볼 것은
$f(x,y,z)$ 으로 표현되는 3변수 3차 다항식입니다.
가장 많이 나오는 유형인 데다, 할 줄 알게 되면 꽤 쉽답니다.
예시를 살펴보죠.
■ 예시1

① 다항식에 대한 분석
문자는 3종류입니다 → 3변수 다항식
식의 항은 총 6개. 모두 문자가 3개씩 곱해져 있으므로. 3차 동차 다항식입니다.
② 특이한 구조 확인
동차 다항식의 경우 특이한 구조가 있을 가능성이 큽니다.
$x→y→z$ 이렇게 한 바퀴 돌려 넣었을 때, 동일한지 확인해 봅니다.

이를 만족한다면 윤환식임을 알 수 있습니다.
③ 대칭식인지 교대식인지 확인
윤환식이라면 대칭식이나 교대식일 수 있죠.
이번엔 $x↔y$ 이렇게 자리를 바꾸어 봅니다.

부호가 바뀌는 것을 보니, 교대식인 것을 알 수 있습니다.
④ 교대식의 성질로 인수분해
3차 교대식은 반드시 $(x-y)(y-z)(z-x)$ 를 인수로 가집니다.
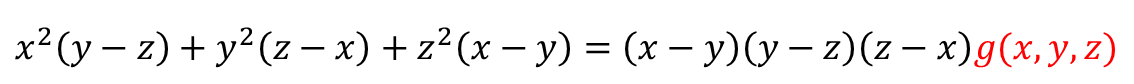
다만, 혹시나 다른 인수가 더 있을 수도 있기 때문에
뒤에 $g(x,y,z)$ 를 곱해서 모르는 식이 있음을 표현해 줍니다.
<참고> 교대식
문자가 여러 개인 다항식[심화2] - ③ 교대식(Alternating Polynomial)
■ 목표 - 교대식이란 - 교대식의 성질 ① - 교대식의 성질 ② 교대식(Alternating Polynomial) 교대는 "번갈아서" 라는 뜻인데요, 마치 껐다켰다하는 "스위치" 같은 이미지를 생각하시면 될 것 같습니다.
indv-wrappedmath.tistory.com
※ 만약, 대칭식이라면 따로 인수를 찾아야 합니다.
$x→y$ 를 대입했을 때, $0$ 이 되는지 확인해 주면 됩니다.
만약 된다면 $(x+y)$ 를 인수로! 그리고,
윤환식이기 때문에, $(x+y)(y+z)(z+x)$ 를 인수로 갖습니다.
⑤ $g(x,y,z)$ 구하기
이 식이 항등식임을 활용합니다.
원래식이 3차식이고, 오른쪽의 $(x-y)(y-z)(z-x)$ 도 이미 3차식이기 때문에,
$g(x,y,z)$ 는 그냥 상수이고, $k$ 라고 놓을 수 있습니다.

역시 항등식이므로,
양쪽에서 특정 항을 비교해 보면 됩니다.
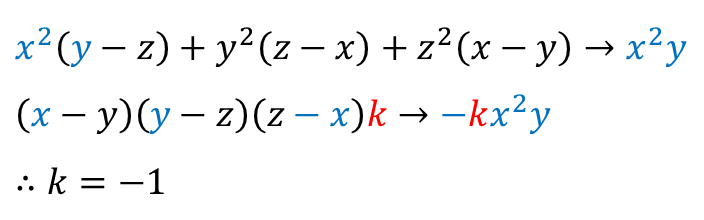
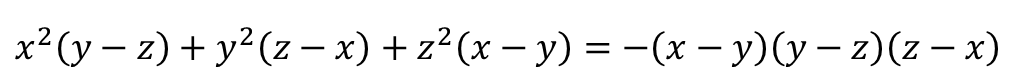
드디어 이렇게 인수분해가 마무리됩니다.
■ 3차 교대식 $f(x, y, z)$ 인수분해 방법
① 차수 확인 : 모든 항이 3차항 → 3차 동차
② 윤환식 확인 : $x→y→z$ 를 대입했을 때, 동일한지.
③ 교대식/대칭식 확인 : $x→y$ 를 대입했을 때, 부호가 바뀌면 교대식, 안 바뀌면 대칭식
④ 인수분해 : 교대식 → $f(x,y,z)=k(x-y)(y-z)(z-x)$
대칭식 → $f(x,y,z)=k(x+y)(y+z)(z+x)$
⑤ 항등식 임을 이용해서 $k$ 찾기
■ 예제1
다음을 인수분해 하시오.
1) $xy(x-y)+yz(y-z)+zx(z-x)$
2) $(x+y+z)(xy+yz+zx)-xyz$
3) $(x+y+z)^3-x^3-y^3-z^3$
4) $xy(x+y)+yz(y+z)+zx(z+x)+2xyz$
5) $(y+z)x^2+(z+x)b^2+(x+y)z^2+2xyz$
(정답)
1) $-(x-y)(y-z)(z-x)$
2) $(x+y)(y+z)(z+x)$
3) $3(x+y)(y+z)(z+x)$
4) $(x+y)(y+z)(z+x)$
5) $(x+y)(y+z)(z+x)$
4차 교대식/대칭식의 인수분해
솔직히 3차 교대식/대칭식 문제도 너무 어렵기 때문에
4차까지 문제로 나오진 않을 거라 생각해요.
그래도 방법은 거의 동일하고,
마지막 한 가지 과정만 추가하면 되니 한번 해보죠.
■ 예시2

① 4차 동차 다항식입니다.
② $x→y→z$ 돌려 넣어도 똑같습니다. 즉, 윤환식입니다.
③ $x↔y$ 자리를 바꾸면, 부호가 바뀝니다. 즉, 교대식입니다.
④ 교대식의 성질로 인수분해가 됩니다.

⑤ $g(x,y,z)$ 를 구해줍니다.
문제는 원래식이 4차식이고, 오른쪽의 $(x-y)(y-z)(z-x)$ 은 3차식이라는 점입니다.
따라서, $g(x,y,z)$ 는 1차식이어야 합니다.
게다가 원래식은 교대식이고, 오른쪽의 $(x-y)(y-z)(z-x)$ 도 교대식입니다.
따라서, $g(x,y,z)$ 는 대칭식이어야 합니다.
(교대식)$\times$(대칭식)=(교대식)이니까요.
<참고> 대칭식
문자가 여러 개인 다항식[심화2] - ② 대칭식(Symmetric Polynomial)
■ 목표 - 대칭식이란 - 대칭식의 성질 - 대칭식의 기본정리 대칭식(Symmetric Polynomial) 대칭이란 무언가가 동등하다는 뜻입니다. 좌우대칭은 좌우의 모양이 같은 것이고, 선대칭은 어떤 선을 기준
indv-wrappedmath.tistory.com
3변수 기본대칭식은 $(x+y+z)$ 이므로,
$g(x,y,z)=k(x+y+z)$ 라고 할 수 있습니다.
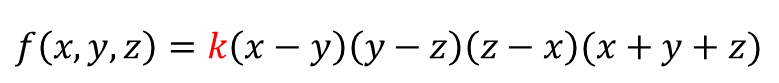
마지막 $k$ 를 구해줍니다.

결국 이렇게 인수분해가 됩니다!

■ 예제2
다음을 인수분해하시오.
1) $x^3(y-z)+y^3(z-x)+z^3(x-y)$
2) $x^2y^2(x-y)+y^2z^2(y-z)+z^2x^2(z-x)$
(정답)
1) $-(x-y)(y-z)(z-x)(x+y+z)$
2) $-(x-y)(y-z)(z-x)(xy+yz+zx)$
마무리
어쩌면 너무너무 어려울 수도 있는
교대식/대칭식의 인수분해가 드디어 끝났어요.
최대한 쉽게 만들어보려 했는데,
역시 복잡해 보이네요.
드디어 인수분해 단원도 끝.
다항식의 연산이 끝입니다!
다음 시간은 새로운 대단원에서 봐요!
'공통수학1 [고1] > 3. 인수분해' 카테고리의 다른 글
| 문자가 여러 개인 다항식[심화2](3/4) - 교대식(Alternating Polynomial) (0) | 2023.03.19 |
|---|---|
| 문자가 여러 개인 다항식[심화2](2/4) - 대칭식(Symmetric Polynomial) (2) | 2023.03.12 |
| 문자가 여러 개인 다항식[심화2](1/4) - 다변수 다항식의 구분 (1) | 2023.03.12 |
| 인수분해 방법(4/4) - 인수정리/조립제법 (0) | 2023.03.12 |
| 문자가 여러 개인 다항식 [심화1] - 인수분해되도록 하는 계수 찾기 (0) | 2022.12.30 |





댓글