■ 목표
- 가우스 기호의 정의
- A.가우스 기호를 포함한 이차방정식 - 인수분해가 될 때
- B.가우스 기호를 포함한 이차방정식 - 범위가 주어질 때

가우스 기호의 정의
가우스 기호는 $\left [x \right ]$
이렇게 생겼습니다.
뜻은 "$x$를 넘지 않는 최대의 정수" 를 구하시오.
입니다.
단순히, 소수점 아래를 버린다는 느낌보다는
"정수가 될 때까지 아래로 내린다" 는 느낌이죠.
예를 들면,
$\left [1.6 \right ]=1$ 이 되고,
$\left [-1.4 \right ]=-2$ 가 됩니다.
좀 더 풀어서 설명하자면,
어떤 정수와 정수 사이,
정확히 한 칸의 범위 안에 있는 모든 수들은
가우스 기호를 만나면,
전부 범위 내의 가장 작은 정수가 되는 것입니다.

■ 가우스 기호

A.가우스 기호를 포함한 이차방정식 - 인수분해될 때
이차방정식에 가우스 기호가 포함된 유형입니다.
그중 첫 번째는 바로
이차방정식이 인수분해가 되는 경우입니다.
■ 예시

이 경우 보이는 모든 $x$ 에 가우스 기호가 있기 때문에,
그냥 $\left [x \right ]$ 를 하나의 문자로 봐도 괜찮습니다.
보기 편하게 치환을 해도 되죠.
그다음 인수분해를 먼저 합니다.
① 인수분해하기

아무튼 결론은
$\left [x \right ]=-3$ 또는 $\left [x \right ]=2$ 입니다.
그래서, 답은 $x$의 범위로 나옵니다.
② 가우스 기호 풀기
$\left [x \right ]=-3$ 라는 말은
$-3 \leq x \leq -2$ 라는 뜻이고,
$\left [x \right ]=2$ 라는 말은
$2 \leq x\leq 3$ 라는 뜻이죠.
답은 $-3 \leq x \leq -2$, $2 \leq x\leq 3$
■ A.가우스 기호를 포함한 이차방정식 - 인수분해될 때
① 인수분해 하기
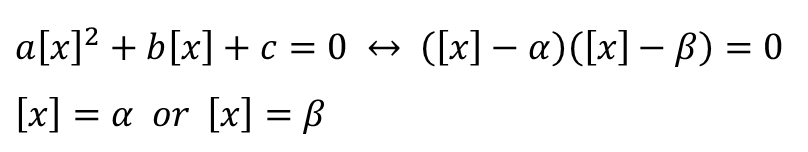
② 가우스 기호 풀기
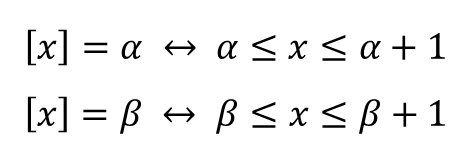
B.가우스 기호를 포함한 이차방정식 - 범위가 주어질 때
두 번째는 $\left [x \right ]$ 를 치환하기도 어렵고,
인수분해가 바로 되지도 않는 유형입니다.
대신, $x$ 의 범위가 주어져있기 때문에,
가우스 기호를 먼저 풀 수 있죠.
■ 예시
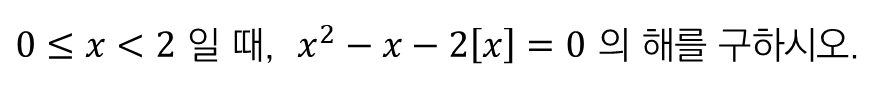
문제가 되는 $\left [x \right ]$ 는 딱 하나 존재합니다.
하지만, 범위가 주어져있다면
$\left [x \right ]$ 는 무조건 정수가 될 수밖에 없습니다.
단, 범위를 "딱 하나 차이나는 정수" 의 범위로 정해줘야만,
가우스 기호를 풀 수 있죠.
① 주어진 범위를 한 칸 범위로 나누기
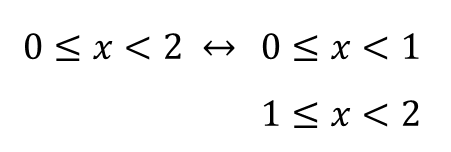
그럼 이 두 가지 범위에 맞게 가우스 기호를 풀 수 있습니다.
② 가우스 기호를 풀고, 이차방정식 해 구하기
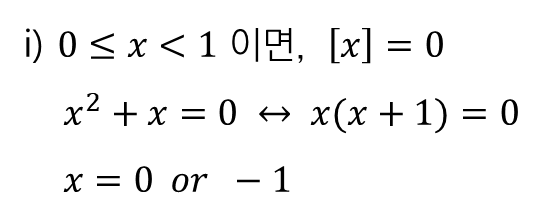
단, 여기서 미리 정한 $x$ 의 범위를 벗어나는 $-1$ 은 답이 아닙니다.

마찬가지로, 범위를 벗어나는 $-2$ 는 답이 아닙니다.
따라서, 해는 $x=0, 1$ 이 됩니다.
■ B.가우스 기호를 포함한 이차방정식 - 범위가 주어질 때
① 주어진 범위를 한 칸 범위로 나누기
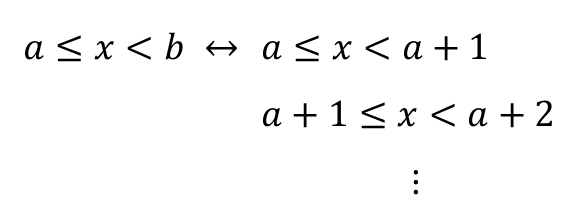
② 가우스 기호를 풀고, 이차방정식 해 구하기
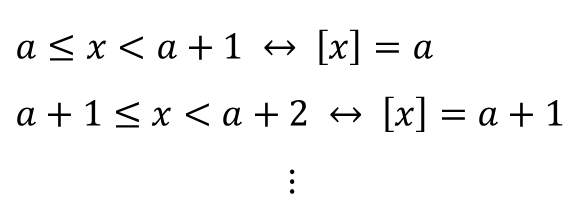
마무리
이차방정식에 가우스 기호가 있으면,
어떻게 풀어야 하는지 살펴봤습니다.
워낙 가우스 기호는 보자마자 겁을 먹기 마련이기 때문에
예시보다 더 어렵게 나오진 않는 편입니다.
하지만, 가우스 기호는 앞으로도
부등식이나 함수에서 계속 쓰일 것이기 때문에,
정의는 잘 숙지하는 것이 중요해요!
'공통수학1 [고1] > 5. 이차방정식' 카테고리의 다른 글
| 이차식의 인수분해 (0) | 2023.07.29 |
|---|---|
| 이차방정식의 판별식(Discriminant) (0) | 2023.07.23 |
| 절댓값을 포함한 이차방정식의 풀이 (0) | 2023.06.25 |
| 절댓값(Absoulte Value) (0) | 2023.06.18 |
| 이차방정식의 풀이 (0) | 2023.06.10 |





댓글