■ 목표
- 이차방정식의 근의 판별(중3 버전)
- 이차방정식의 근의 판별(고1 버전)

개요
근의 공식을 찾아낸 이상
이제 이차방정식의 근은 무조건 구할 수 있습니다.
<참고> 이차방정식의 풀이
이차방정식의 풀이
■ 목표 - 실근과 허근 - 이차방정식의 풀이 - ① 인수분해 이용하기 - ② 완전제곱식 이용하기 - ③ 근의 공식 이용하기 실근과 허근 이차방정식은 이미 중학교 3-1 과정에서 한번 배웠습니다. 근
indv-wrappedmath.tistory.com
하지만, 근을 구하는 게 그다지 중요하지 않을 때도 많습니다.
근이 너무 복잡하다면, 오히려 계산이 힘들어지기 때문이죠.
그래서 굳이 근을 구하지 않고,
이차방정식의 여러 정보들을 알아내는 방법을 살펴볼 것입니다.
그 첫 번째는 근의 판별입니다.
이차방정식의 근의 판별 (중3 버전)
판별식(Discriminant)은
이미 중학교 3-1 과정에서 배운 내용입니다.
이차방정식을 보고 바로 근의 개수를 알 수 있는 식이죠.
그건 근의 공식 덕분입니다.

여기서 근의 개수를 결정하는 부분은
바로 이것입니다.

① 앞의
근은 보통 두 개입니다.
② 하지만, 만약
③ 그리고
아예 근은 존재하지 않게 됩니다.
중3 때만 해도
모든 수는 제곱하면 양수가 되므로,
루트 안에는 "절대 음수가 올 수 없다" 라고 배웠기 때문이죠.
결국 "루트 안에 있는 식" 이 어떤 값인지에 따라
근의 개수가 달라집니다.
이 루트 안의 식인
근을 판별하는 식 즉, 판별식(Discriminant)이라 하고,
기호
■ 이차방정식의 근의 판별 (중3 버전)

이차방정식의 근의 판별(고1 버전)
우리는 고1이 되면서 수의 체계를 확장했고,
제곱하면 음수가 되는 수인 허수를 배웠습니다.
<참고> 수 체계의 확장
수 체계의 확장
■ 목표 - 수 체계의 확장 - 수 집합의 포함관계 수 체계의 확장 수 체계(Number System)는 우리가 배워온 모든 숫자들이 어떤 성질들을 가지는지, 어떤 연산이 가능한지 등을 연구한 것이에요. 그 과
indv-wrappedmath.tistory.com
즉, 루트 안에 음수를 쓸 수 있다는 걸 알았죠.
근이 존재하지 않는 것이 아니라
사실 허수인 근이 존재했던 것입니다.
따라서, 이제 이차방정식의 근의 판별은
단순히 개수뿐 아니라
근이 실수인지 허수인지도 구분을 해주어야 합니다.
■ 이차방정식의 근의 판별 (고1 버전)

※ 한 가지 주의할 점은 중근인데,
이 경우 근의 개수가 하나라고 생각하기 쉽죠.
중근은 완전제곱식을 풀 때 나오는데,
의미는 "중복된 근" 이라는 뜻입니다.
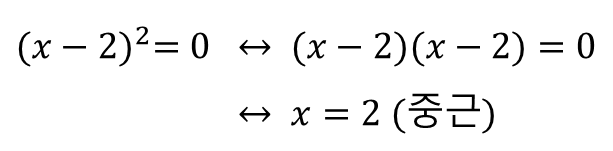
똑같은 근인
하나만 써주고 "중근" 이라고 써주는 것입니다.
즉, "서로 같은 실근 2개" 라는 의미와 같죠.
그래서 이차방정식은
서로 다른 두 실근이든, 중복된 두 개의 근이든, 서로 다른 두 허근이든,
"무조건 근 2개" 를 갖는다는 뜻입니다.
마무리
이차방정식에 대한 정보 찾아내기 첫 번째,
근의 판별이었습니다.
한번 배웠었던 내용에 조금 확장만 된 것이니
크게 어렵진 않았을 거예요.
여기까지!
'공통수학1 [고1] > 5. 이차방정식' 카테고리의 다른 글
| 이차방정식의 근과 계수의 관계 (0) | 2023.08.05 |
|---|---|
| 이차식의 인수분해 (0) | 2023.07.29 |
| 가우스 기호를 포함한 이차방정식의 풀이 (1) | 2023.07.15 |
| 절댓값을 포함한 이차방정식의 풀이 (0) | 2023.06.25 |
| 절댓값(Absoulte Value) (0) | 2023.06.18 |





댓글