■ 목표
- 절댓값(Absolute Value)
- 절댓값이 포함된 방정식
개요
평범한 방정식이나 부등식을
어렵고 복잡한 문제로 만드는 대표적인 요인.
그 중 첫번째가 바로 절댓값입니다.
단순히 이 문제유형을 푸는 방법을 아는 것보단,
절댓값의 정확한 의미를 이해하는 것이 중요합니다.
절댓값(Absolute Value)
많은 학생들이 절댓값의 정의는 몰라도
푸는 방법은 압니다.
기호 $| |$ 가
"무조건 양수로 바꿔주는 기호" 라고 알고 있기 때문이죠.
예를 들면, $|1|=1$, $|-1|=1$ 이렇게
절댓값 기호 안쪽의 수가
양수라면 그대로
음수라면 부호를 바꿔 써주면 됩니다.
■ $x$ 의 절댓값의 정의와 성질
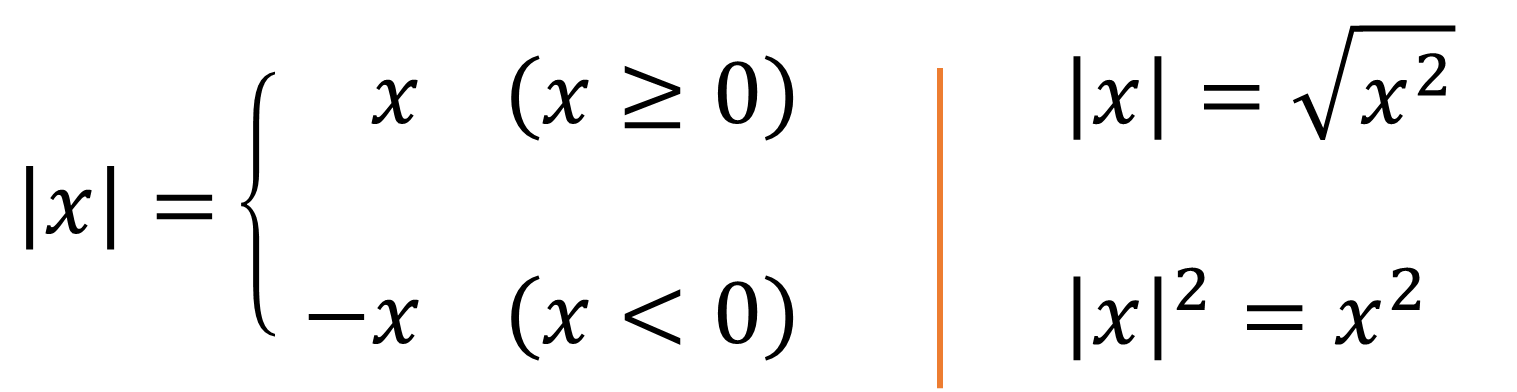
$-x$ 는 음수처럼 보이지만
$x$ 가 음수라면 $-x$ 가 양수인 겁니다.
즉, 절댓값은 무조건 양수가 된다는 뜻이죠.
$x$ 의 부호에 따라 생긴 모습은 다르지만,
제곱하면 똑같아진다는 성질도 갖고있죠.
근데 절댓값 기호는
왜 "양수로 바꿔주는 기호" 가 된 걸까요?
절댓값이란 수직선에서
"원점으로부터의 거리" 를 의미합니다.
방향은 생각하지 말고,
얼마나 멀리 떨어져있는 지 절대적인 거리값만 생각하자는 거죠.

그래서 $|1|$ 은 "원점과 $1$ 사이의 거리",
$|-1|$ 은 "원점과 $-1$ 사이의 거리" 이므로,
$1$ 이 됩니다.
거리가 음수일 수는 없기 때문에
모든 수의 절댓값은 항상 양수가 되는 것이죠.
반대로 원점으로부터의 거리가 $1$ 인 점이 뭔지
물어본다면 답은 $1$ 과 $-1$ 이 됩니다.
이를 기호로 쓰면 이렇게 되죠.
$|x|=1$ 이면 $x=1, -1$ 이다.
■ 원점으로부터의 거리가 $a$ 인 점 $x$

수직선 위의 두 점 사이의 거리를 구할 때도,
절댓값을 사용하면 편리합니다.
수직선 위에서 거리는
$2$ 와 $5$ 사이의 거리는 $5-2=3$ 이고,
$9$ 와 $3$ 사이의 거리는 $9-3=6$ 인 것처럼,
큰 수에서 작은 수를 빼주면 됩니다.
하지만, "$a$ 와 $b$ 사이의 거리" 처럼
둘 중에 누가 더 큰 지를 모른다면, 어떻게 할까요?
이때, 절댓값을 이용해서
거리를 $|a-b|$ 혹은 $|b-a|$ 로 써주면 됩니다.

어차피 $a$ 가 더 크든 더 작든
절댓값은 무조건 양수가 되기 때문이죠.
절댓값이 포함된 방정식
자 이제 실전입니다.
방정식을 어렵게 만들고 싶다면,
적당히 절댓값만 씌우면 완성입니다.

우리가 배운 절댓값의 정의를 이용해서
이 문제를 세 가지 관점으로 풀어볼게요.
■ 예시
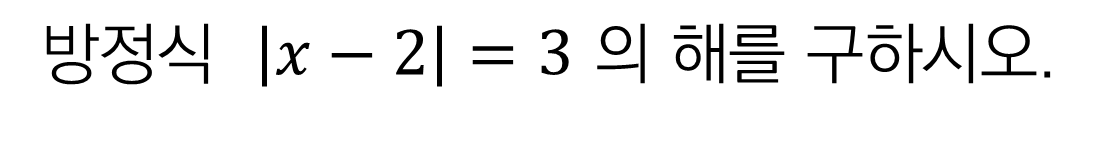
A. 양수로 바꿔주는 기호

가장 익숙한 방법이죠.
$x-2$ 가 양수인지 음수인지 모르기 때문에
두 가지 경우로 나누어서 식을 풉니다.
1) $x\geq2$ 이면, 양수이므로 그대로 $x-2$ 가 됩니다.
$x-2=3$ 이므로, $x=5$ 입니다.
2) $x<2$ 이면, 음수이므로 부호를 바꿔 $-x+2$ 가 됩니다.
$-x+2=3$ 이므로, $x=-1$ 입니다.
답은 $x=-1, 5$
B. 원점으로부터의 거리

원점으로부터 점 $(x-2)$ 까지의 거리가 $3$ 이라는 뜻입니다.
원점에서 거리가 $3$ 인 점은 $-3, 3$ 딱 두 개죠.

따라서, $x-2=-3$, $x-2=3$ 이고,
답은 $x=-1, 5$ 입니다.
C. 두 점 사이의 거리

점 $x$ 와 점 $2$ 사이의 거리가 $3$ 이라는 뜻입니다.
점 $2$ 에서 거리가 $3$ 인 점은 $-1, 5$ 딱 두 개죠.

따라서, $x=-1$, $x=5$ 입니다.
결국 거리를 이용한 방법이
굉장히 편리하다는 것을 알 수 있죠.
마무리
절댓값 자체로는 크게 어렵지 않지만,
방정식과 부등식, 함수에 포함되면서
많은 학생들의 머리를 아프게 하는 개념이죠.
개념을 한번 정확하게 이해하면
어려운 문제들도 잘 이해해낼 수 있으니
꼭 알아두는 것이 좋습니다!
'공통수학1 [고1] > 5. 이차방정식' 카테고리의 다른 글
| 이차식의 인수분해 (0) | 2023.07.29 |
|---|---|
| 이차방정식의 판별식(Discriminant) (0) | 2023.07.23 |
| 가우스 기호를 포함한 이차방정식의 풀이 (1) | 2023.07.15 |
| 절댓값을 포함한 이차방정식의 풀이 (0) | 2023.06.25 |
| 이차방정식의 풀이 (0) | 2023.06.10 |





댓글