이차방정식의 풀이

■ 목표

- 실근과 허근

- 이차방정식의 풀이

- ① 인수분해 이용하기

- ② 완전제곱식 이용하기

- ③ 근의 공식 이용하기

 

 

 

 

 

실근과 허근

 

이차방정식은 이미

중학교 3-1 과정에서 한번 배웠습니다.

 

 

근데 수(상)에서는 복소수를 배운 후,

정확히는  "음수의 제곱근이 존재한다" 는 사실을 배운 후에

다시 이차방정식을 배우게 되죠.

 

 

따라서, 이제는 이런 이차방정식의 근도 구할 수 있습니다.

 

 

이처럼 근이 허수인 경우엔 허근이라고 부르고,

근이 실수인 경우엔 실근이라고 부릅니다.

 

 

근의 범위가 확장된 만큼

조금 더 다양한 이차방정식들을 풀게 될 텐데요,

처음은 복습한다는 느낌으로 가볍게 보면 되겠습니다.

 

 

 

이차방정식의 풀이

 

방정식이란  "특정값일 때만 성립하는 등식" 입니다.

 

 

즉, 방정식을 푼다는 것은

등식을 성립하게 하는 특정값인

해(근)를 구하는 것입니다.

 

 

<참고> 방정식

방정식과 항등식

 

 

이차방정식은

이차식+방정식이겠죠.

 

 

즉, 이차방정식의 풀이란

이차식이  $0$ 이 되도록 하는 해 $x$ 를 구하는 것입니다.

 

 

 

① 인수분해 이용하기

 

두 수의 곱이  $0$ 이라면 둘 중 하나는  $0$ 이죠.

 

 

그래서 만약 이차식이 인수분해만 된다면

이차방정식의 풀이는 아주 쉽습니다.

 

 

■ 인수분해를 이용한 이차방정식의 풀이

 

 

두 가지 인수분해 공식의 모양을

잘 기억하고 있으면 쉽게 인수분해를 할 수 있습니다.

 

 

 

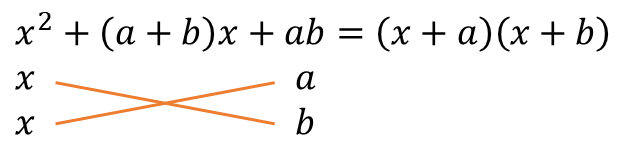
예를 들면,  $x^2+2x-3$,  $x^2-5x+6$ 등이 있죠.

 

 

 

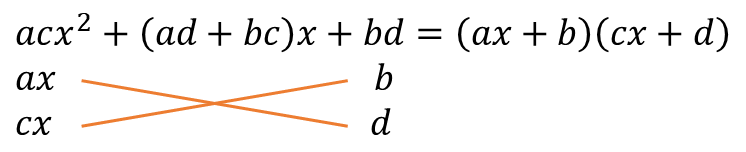
예를 들면,  $2x^2-5x-3$,  $3x^2+8x+4$ 등이 있습니다.

 

 

 

② 완전제곱식 이용하기

 

제곱해서  $A$ 가 되는 수는

제곱근을 이용해 쉽게 구할 수 있습니다.

 

 

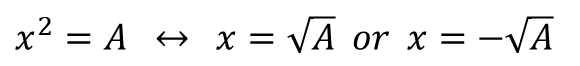
그래서 이차식이 인수분해가 안 된다면

완전제곱식을 만들어 풀 수 있습니다.

 

 

■ 완전제곱식을 이용한 이차방정식의 풀이

​

 

$x^2$ 의 계수가  $1$ 일 때,

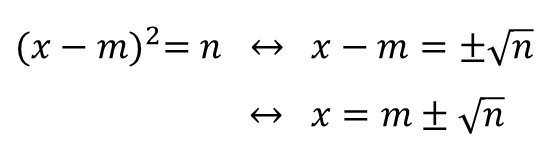
완전제곱식을 만드는 연습이 필요합니다.

 

 

 

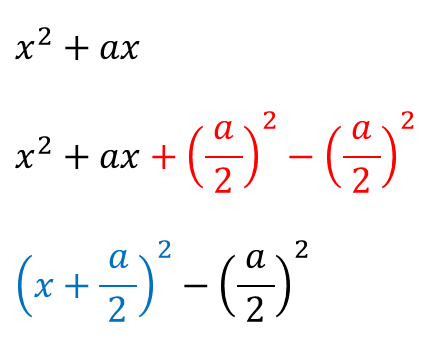
예를 들어,  $x^2-6x$ 를 보고,

$x^2-6x+9-9=(x-3)^2-9$ 로 만드는 연습이죠.

 

 

 

③ 근의 공식 이용하기

 

한국인이라면 자다가도 외운다는

바로 그 근의 공식입니다.

 

 

인수분해가 안될 때마다

매번 완전제곱식을 만드는 게 너무 귀찮죠.

 

 

그래서 그냥

$ax^2+bx+c=0$ 에서 완전제곱식을 이용해

근을 미리 구해버린 겁니다.

 

 

덕분에 근의 공식은

$a, b, c$ 만 뭔지 알면 바로 대입해서

근을 구할 수 있는 공식입니다.

 

 

■ 이차방정식의 근의 공식

근의 공식

 

​(근의 공식 유도과정)

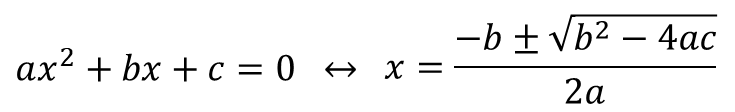
근의 공식 유도과정

 

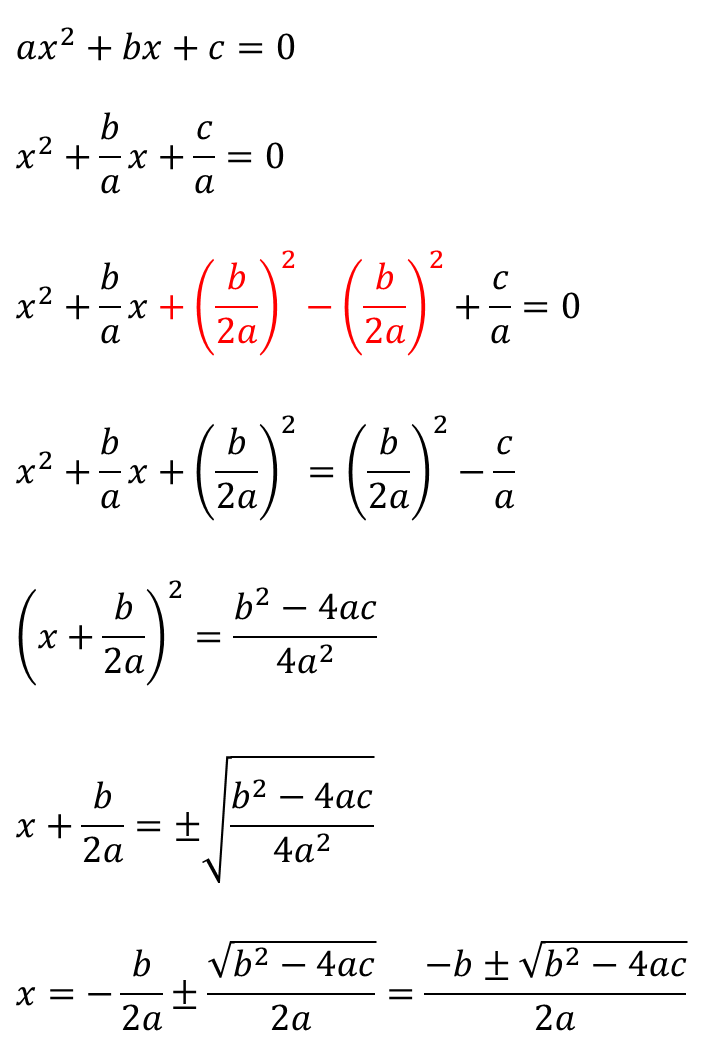
이 때, 만약  $b$ 가 짝수라면 근의 공식을

조금 더 간결하게 쓸 수 있습니다.

 

 

$b$ 대신에  $2b'$ 을 대입해보면 이렇게 됩니다.

 

 

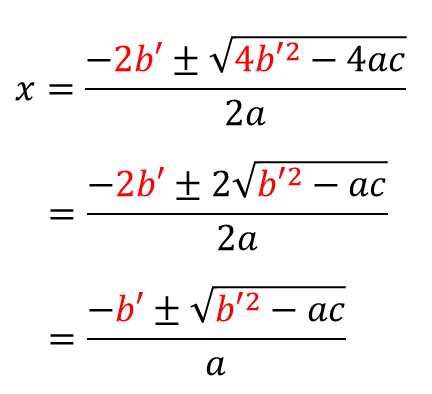
■ 이차방정식의 근의 공식 (b가 짝수일 때)

근의 공식(b가 짝수일 때)

​

 

 

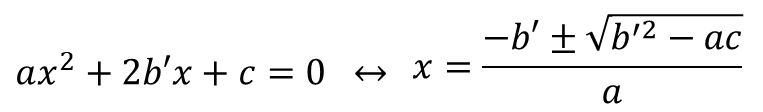
마무리

 

근의 공식을 찾아냄으로써

평범한 이차방정식은 전부 근을 찾아낼 수 있게 됩니다.

 

다음엔 평범하지 않은

절댓값이나 가우스 기호를 포함한 특이한 이차방정식에 대해 풀어볼게요.