■ 목표
- 이차방정식의 근과 계수의 관계
- 근과 계수의 관계 증명

개요
우리는 판별식에 이어 근을 구하지 않고도,
이차방정식의 중요한 성질들을 알아내는 방법을 배우고 있습니다.
<참고> 이차방정식의 판별식
이차방정식의 판별식(Discriminant)
■ 목표 - 이차방정식의 근의 판별(중3 버전) - 이차방정식의 근의 판별(고1 버전) 개요 근의 공식을 찾아낸 이상 이제 이차방정식의 근은 무조건 구할 수 있습니다. 이차방정식의 풀이 이차방정
indv-wrappedmath.tistory.com
이번엔 그 두 번째인 근과 계수의 관계입니다.
이차방정식의 계수만을 이용해서 두 근에 대한 정보를 알 수 있는
아주 훌륭한 방법이죠.
줄여서 "근계관" 이라고 많이들 부르는데요.
줄임말까지 있다는 건
그만큼 활용도가 아주 높다는 거겠죠?
이차방정식의 근과 계수의 관계
이차방정식은 보통 이렇게 생겼습니다.
$$ax^2 + bx + c = 0$$
이 이차방정식의 근을 $α$ 와 $β$ 라고 해봅시다.
두 근 $α$ 와 $β$ 를 직접 구하지 않고도, 계수인 $a$, $b$, $c$ 를 이용하면,
두 근의 합인 $\alpha+\beta$ 와
두 근의 곱인 $\alpha\beta$ 는 아주 쉽게 구할 수 있습니다.
‘두 근의 관계를 계수를 이용하여 구한다.’
그래서 이를 "근과 계수의 관계" 라고 합니다.
■ 이차방정식의 근과 계수의 관계
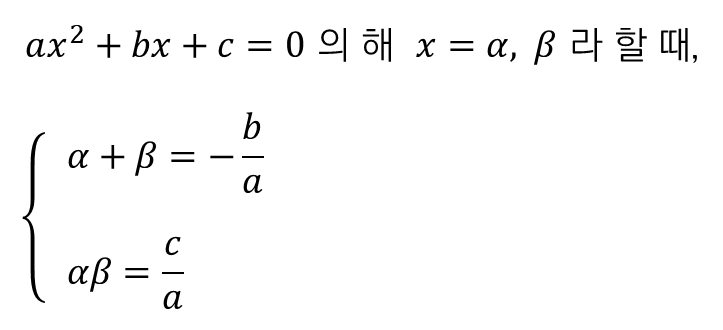
그냥 식에 $a$, $b$, $c$ 를 대입만 하면 되죠.
근데 왜 이런 관계가 성립하는 걸까요??
이차방정식의 근과 계수의 관계 증명
■ 근의 공식을 통한 증명
근의 공식을 통해 근을 구해보면 다음과 같습니다.
$$x=\frac{-b \pm \sqrt{b^2 - 4ac}} {2a}$$
근은 확실히 복잡해 보이죠.
하지만, 두 근을 더하거나 곱한다면
계산 결과는 굉장히 단순해집니다.
① 두 근의 합 구하기
$$\begin{align} \alpha+\beta &=\frac{-b + \sqrt{b^2 - 4ac}} {2a} + \frac{-b - \sqrt{b^2 - 4ac}} {2a} \\ \\ &=-\frac{2b} {2a} \\ \\ &=-\frac{b} {a} \end{align}$$
$\pm$ 부호 때문에 루트가 있는 항은 사라지고, $-\dfrac{b} {a}$ 만 남게 되죠.
② 두 근의 곱 구하기
$$\begin{align*}\alpha \beta &= \left(\frac{-b + \sqrt{b^2 - 4ac}} {2a}\right) \left(\frac{-b - \sqrt{b^2 - 4ac}} {2a}\right) \\\\&= \frac{(-b)^2 - (\sqrt{b^2 - 4ac})^2} {(2a)^2} \\\\&= \frac{b^2 - (b^2 - 4ac)} {4a^2} \\\\&= \frac{4ac} {4a^2} \\\\&= \frac{c} {a}\end{align*}$$
합차공식에 의해 많은 항이 사라지고, $\dfrac{c}{a}$ 만 남습니다.
■ 인수분해를 통한 증명
이차방정식의 근을 $\alpha$와 $\beta$라고 할 때,
주어진 이차식을 인수분해하면 다음과 같습니다.
$$ax^2 + bx + c = a(x - \alpha)(x - \beta) $$
이 식을 풀면 다음과 같죠.
$$
\begin{align*}
ax^2 + bx + c &= a\{x^2 - (\alpha + \beta)x + \alpha \beta\} \\\\
x^2 + \frac{b}{a}x + \frac{c}{a} &= x^2 - (\alpha + \beta)x + \alpha \beta
\end{align*}
$$
이제 양쪽을 비교해 보면 알 수 있습니다.
$$\begin{align} \alpha+\beta &= -\frac{b}{a}\\\\ \alpha\beta &= \frac{c}{a} \end{align} $$
마무리
근과 계수의 관계는
복잡한 계산이 없이 이차방정식의 성질을 파악하고,
문제를 더욱 효과적으로 해결할 수 있게 해주는 멋진 방법입니다.
이차방정식뿐 아니라, 더 확장되어
비에트의 정리(Viète’s theorem) 라는 이름으로써
많은 다항식에서 활용된답니다.
여기까지!
'공통수학1 [고1] > 5. 이차방정식' 카테고리의 다른 글
| 이차방정식의 작성 (0) | 2023.08.12 |
|---|---|
| 특정 식의 값 구하기 (0) | 2023.08.06 |
| 이차식의 인수분해 (0) | 2023.07.29 |
| 이차방정식의 판별식(Discriminant) (0) | 2023.07.23 |
| 가우스 기호를 포함한 이차방정식의 풀이 (0) | 2023.07.15 |





댓글