이차방정식의 근과 식의 변형

■ 목표

- 근이 변하면 식은 어떻게 바뀔까?

- $f(x)=0$ 과  $f(ax+b)=0$ 의 관계

 

 

 

 

 

개요

 

지난 시간에

$\alpha$ 와  $\beta$ 를 가진 이차방정식을 알려주고,

$\alpha -1$ 과 $\beta -1$ 을 근으로 하는 이차방정식 찾기를 해봤습니다.

 

 

 

<참고> 이차방정식의 작성

이차방정식의 작성

 

 

그런데 단순히, 근이  $-1$ 되었을 뿐인데,

식 찾는 건 왜 이렇게 힘들까요?

일일이 근과 계수의 관계를 써야만 하는 걸까요?

 

 

그래서 이번엔

근이 변형되었을 때, 식은 어떻게 바뀌는 지를 살펴볼까 해요.

 

 

 

근이 변하면 식은 어떻게 바뀔까?

 

첫 번째는 근에 어떤 상수가 "더해진 경우" 입니다.

 

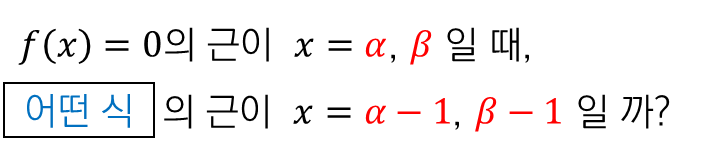
먼저,  $f(x)=0$ 의 근이  $\alpha$,  $\beta$ 라는 건,

$f(x)=(x-\alpha )(x-\beta )=0$ 이라는 것을 알 수 있습니다.

 

 

그리고 우리가 찾고 싶은 식의 근은

$x=\alpha -1$,  $\beta -1$ 이죠.

이는 잘 생각해 보면

$x+1=\alpha ,$  $\beta$ 라는 말과 같습니다!

 

 

식으로 표현하면,

$($$x+1$$-\alpha )($$x+1$$-\beta )=0$ 이죠.

 

 

즉, 원래 있던 이차방정식에

$x$ 대신  $x+1$ 만 넣어준다면,

우리가 찾고 싶었던

$x+1=\alpha$,  $\beta$ 인 식이 됩니다.

 

 

즉,  $x=\alpha -1$,  $\beta -1$ 를 근으로 갖는 식은

$f($$x+1$$)=0$ 인거죠.

 

---

 

이번엔 어떤 상수가 "곱해진 경우"입니다.

 

 

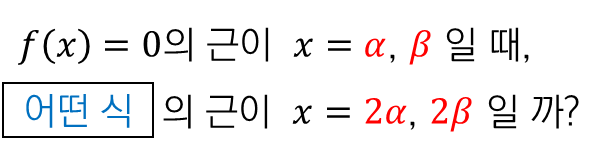
아까와 마찬가지로

$x=2\alpha$,  $2\beta$ 라는 건,

 

${\displaystyle \frac{x}{2}}=\alpha ,$  $\beta$ 라는 말과 같습니다.

 

 

따라서, 우리가 찾는 식은

 

$({\displaystyle \frac{x}{2}}-\alpha )({\displaystyle \frac{x}{2}}-\beta )=0$ 이죠.

 

 

즉, 원래 식에서  $x$ 대신  ${\displaystyle \frac{x}{2}}$ 만 넣어준,

 

$f\left({\displaystyle \frac{x}{2}}\right)=0$ 입니다.

 

---

 

위의 두 가지 내용을 종합하면

근이 아무리 이상하게 변하더라도,

원래 식을 이용해서 새로운 식을 찾아낼 수 있습니다.

 

 

■ 근이 변형된 이차방정식의 작성

 

​

 

 

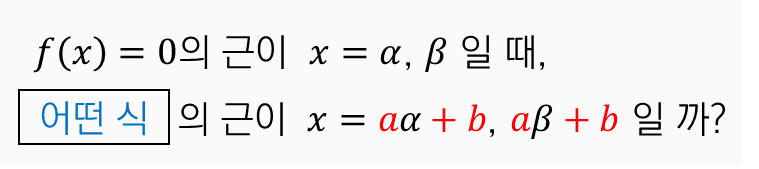
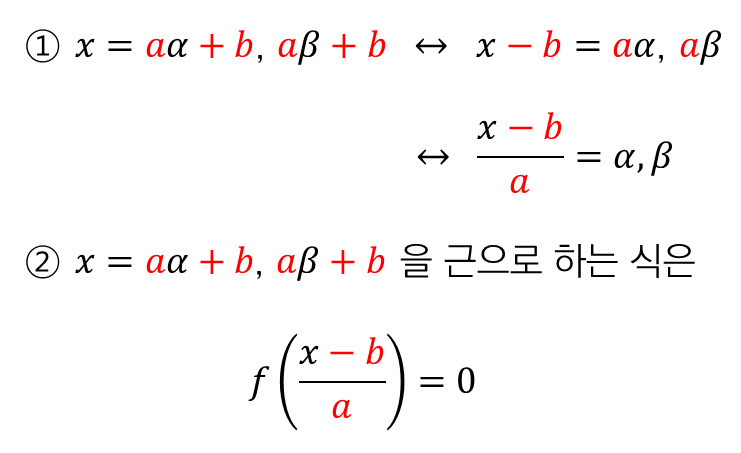
 $f(x)=0$ 과  $f(ax+b)=0$ 의 관계

 

지금까지 쭉 살펴보니

"$f(x)=0$ 의 근이  $x=\alpha$,  $\beta$" 라는 조건에서

$f( )=0$ 은 변하지 않습니다.

 

 

따라서,  $( )$ 안에는

$\alpha$,  $\beta$ 가 들어가야만  $0$ 이 됩니다.

그래서 안쪽의  $x$ 가 바뀌면, 근도 모습이 바뀌는 것이죠.

 

 

$f(x+1)=0$ 에서는  $x+1=\alpha$,  $\beta$ 이므로,

$x=\alpha -1$,  $\beta -1$

 

$f(2x)=0$ 에서는  $2x=\alpha$,  $\beta$ 이므로,

$x={\displaystyle \frac{\alpha }{2}}$,  ${\displaystyle \frac{\beta }{2}}$

 

$f(2x+1)=0$ 에서는  $2x+1=\alpha$,  $\beta$ 이므로,

$x={\displaystyle \frac{\alpha -1}{2}}$,  ${\displaystyle \frac{\beta -1}{2}}$

 

이렇게 되죠.

 

 

즉,  $f(ax+b)=0$ 의 근을 구하는 방법도 같습니다.

 

$ax+b=\alpha$,  $\beta$ 가 되어야 하기 때문에,

 

근은  $x={\displaystyle \frac{\alpha -b}{a}}$,  ${\displaystyle \frac{\beta -b}{a}}$ 가 됩니다.

 

 

■  $f(x)=0$ 과  $f(ax+b)=0$ 의 관계

 

 

 

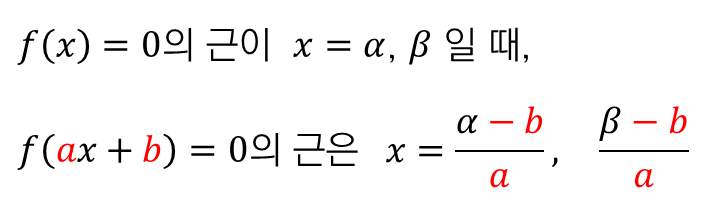
마무리

 

꽤 이해하기 어려울 수도 있고,

실제로 문제에서 어렵게 출제되기도 합니다.

하지만, 그만큼 이해하면 확실하게 큰 힘이 되는

중요한 내용이랍니다.