■ 목표
- 이차방정식과 나머지정리
- 나머지가 상수인 경우
- 나머지가 일차식인 경우

이차방정식과 나머지정리
우리는 주어진 정보를 이용해서
이차방정식을 찾아내는 문제를 계속 풀고 있습니다.
그중 가장 기본적인 형태가
근을 알려주고 이차방정식을 찾는 것이었죠.
<참고> 이차방정식의 작성
이차방정식의 작성
■ 목표 - 인수정리 이용하기 - 근과 계수의 관계 이용하기 개요 이차방정식의 작성 유형은 조건에 맞는 '이차방정식을 찾아내는 것' 이 목표입니다. 직접 근을 알려주거나, 근에 대한 정보를 주
indv-wrappedmath.tistory.com
근데 인수정리는 원래
다항식의 나눗셈 과정에서 나온 정리예요.
나눗셈과 관련이 깊습니다.
<인수정리>
인수정리
■ 목표 - 인수 vs 약수 - 인수정리 이해하기 인수 vs 약수 "소인수분해", "인수분해" 뭔가 자연스럽게 사용은 하고 있었지만 인수가 정확히 뭘까요? 인수(Factor)는 약수(Divisor)와 비슷한 단어이긴 합
indv-wrappedmath.tistory.com
$f(x)=0$ 의 근이 $\alpha$, $\beta$ 라는 건,
$f(x)$ 가 $(x-\alpha)(x-\beta)$ 를 "인수로 갖는다" 는 뜻이고,
$f(x)$ 가 $(x-\alpha)(x-\beta)$ 로 "나누어 떨어진다" 는 말도 됩니다.

이차식을 이차식으로 나누어서,
몫은 상수인 $a$, 나머지가 $0$ 이기 때문에,
$f(x)=a(x-\alpha)(x-\beta)$ 가 되는 것이죠.
그렇다면, 이차식
$(x-\alpha)(x-\beta)$ 로 나눈 나머지가
$0$ 이 아닌 경우도 있겠죠?
바로, 나머지가 상수이거나 일차식인 경우입니다.
나머지정리에 따라서 말이죠.
나머지가 상수인 경우
$f(x)$ 가 이렇게 생겼다고 해볼까요?
$f(x)=a(x-\alpha)(x-\beta)+k$
$f(x)$ 는 이차식이고,
$(x-\alpha)(x-\beta)$ 로 나눈 나머지가 $k$ 이죠.
이 조건을 간단하게
$f(\alpha)=f(\beta)=k$ 로 표현할 수 있습니다.
문제에서는 반대로
$f(\alpha)=f(\beta)=k$ 라는 조건을 보고
$f(x)$ 가 어떤 모양인지를 생각해내는 것이 필요합니다.
■ 예시

우리가 찾고자하는 것은 이차식 $f(x)$ 입니다.
$x^2$ 의 계수가 $2$ 이고,
$f(\alpha)=f(\beta)=3$ 이라는 조건에서
$f(x)=2(x-\alpha)(x-\beta)+3$ 임을 알 수 있죠.
그리고 $x^2-2x+2$ 의 근이 $\alpha$, $\beta$ 이기 때문에
$x^2-2x+2=(x-\alpha)(x-\beta)$ 입니다.
즉, $f(x)=2(x^2-2x+2)+3$ 이고
$f(1)=2+3=5$ 입니다.
■ 나머지가 상수인 이차식 $f(x)$

나머지가 일차식인 경우
이번엔 $f(x)$ 가 이렇게 생겼습니다.
$f(x)=a(x-\alpha)(x-\beta)+x+1$
$f(x)$ 는 이차식이고,
$(x-\alpha)(x-\beta)$ 로 나눈 나머지가 $x+1$ 이죠.
이 경우엔 $\alpha$ 를 넣으면, $\alpha$ 에 대한 식이 나옵니다.
$f(\alpha)=\alpha+1$, $f(\beta)=\beta+1$ 이죠.
■ 예시1

$\alpha$ 와 $\beta$ 를 넣었을 때,
$\alpha$ 와 $\beta$ 에 대한 식이 나오죠.
그래서, $f(x)$ 는 다음과 같이 생겼습니다.
$f(x)=2(x-\alpha)(x-\beta)+2-x$
위의 예제와 마찬가지로,
$x^2-2x+2=(x-\alpha)(x-\beta)$ 이므로,
$f(x)=2(x^2-2x+2)+2-x$
$f(1)=2+2-1=3$ 입니다.
이 문제가 익숙해진다면,
주어진 조건이 너무 직관적이어서
조금 숨겨놓을 수도 있답니다.
■ 예시2

아까와 비슷하지만,
$\alpha$ 를 넣으면, $\beta$ 가 나오고
$\beta$ 를 넣으면, $\alpha$ 가 나오죠.
엄청 특별한 성질이 있는 게 아니라
$\alpha$ 와 $\beta$ 의 관계식을 이용해서
교묘하게 숨겨놓았을 뿐입니다.
바로 근과 계수의 관계입니다.
주어진 이차방정식에서 두 근의 합,
$\alpha+\beta=2$ 라는 걸 알 수 있습니다.
즉, $\beta=2-\alpha$, $\alpha=2-\beta$ 인거죠.
$f(\alpha)=2-\alpha$
$f(\beta)=2-\beta$
결국은 예제1과 완전히 동일한 문제가 됩니다.
■ 나머지가 일차식인 이차식 $f(x)$
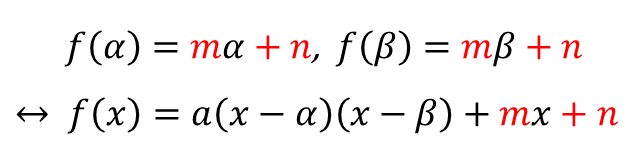
마무리
이차방정식에서
가장 어려운 문제로도 출제되는 유형이죠.
낯설지만 자주 보다 보면
앞으로도 구조가 잘 보일 거예요!
여기까지!
'공통수학1 [고1] > 5. 이차방정식' 카테고리의 다른 글
| 이차방정식의 켤레근의 성질 (0) | 2023.08.26 |
|---|---|
| 이차방정식의 근과 식의 변형 (0) | 2023.08.13 |
| 이차방정식의 작성 (0) | 2023.08.12 |
| 특정 식의 값 구하기 (0) | 2023.08.06 |
| 이차방정식의 근과 계수의 관계 (0) | 2023.08.05 |





댓글