■ 목표
- 이차함수의 그래프의 꼭짓점 알아보기
- 이차함수의 그래프의 절편 알아보기

개요
어떤 함수의 그래프를 그릴 때 필요한 건,
몇 개의 점의 좌표를 정확히 찍는 것입니다.
이차함수에서는 세 가지 점,
꼭짓점과 $x$절편 그리고 $y$절편을 표시할 수 있어요.
이 점들이 뭔지 그리고 어떻게 찾는지에 대해
알아보도록 하겠습니다.
이차함수의 그래프의 꼭짓점
꼭짓점은 포물선 모양에서 생기는 점으로,
이차함수의 가장 대표적인 점입니다.
포물선을 따라 움직였을 때,
"가장 낮은" 골짜기나 "가장 높은" 꼭대기에 있는 점이죠.
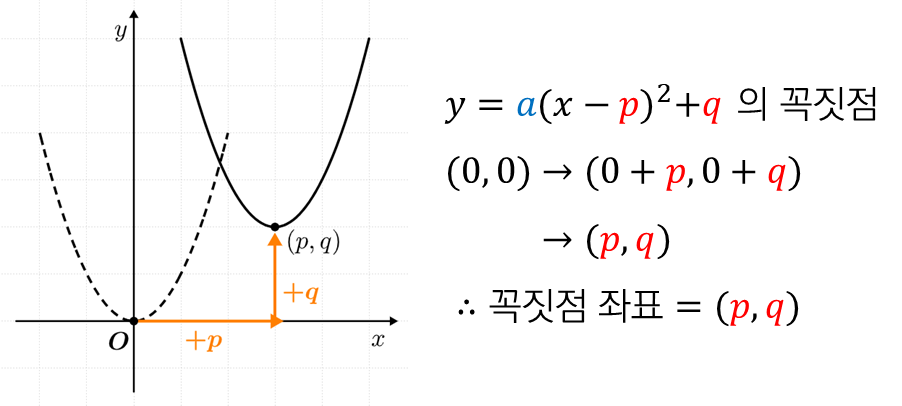
만약, 표준형의 이차함수 식을 알고 있다면,
꼭짓점의 좌표를 바로 구할 수 있습니다.
$y=x^2$ 의 꼭짓점이 원점이라는 것과
평행이동을 이용해서 말이죠.

예를 들어,
$y=(x-3)^2+2$ 는 $y=x^2$ 을
오른쪽으로 $+3$ 만큼, 위쪽으로 $+2$ 만큼
평행이동한 그래프이죠.
따라서, 꼭짓점도 원점에서 똑같이 평행이동한
$(3, 2)$ 가 됩니다.
■ 이차함수의 그래프의 꼭짓점
이차함수의 그래프의 절편
절편의 정의는 "잘라내는 점" 입니다.
즉, $x$절편과 $y$절편은 그래프가 각각
$x$축과 $y$축을 잘라내는 점이죠.
사실 대부분의 함수가 가지고 있는 점입니다.
그래프를 좌표평면에 그리다 보면,
웬만해선 $x$축이나 $y$축과 지날 수밖에 없기 때문이죠.
이차함수도 보통 그렇습니다.

하지만, 절편은 항상 존재하는 건 아닙니다.
폭과 방향, 평행이동에 따라 달라질 수도 있죠.
먼저, 이차함수의 $y$절편은 항상 존재합니다.
꼭짓점을 아무 데나 두고, 폭을 아무리 변화시켜도
$y$축은 무조건 지날 수밖에 없기 때문이죠.

하지만, 이차함수의 $x$절편은 다릅니다.
내려갔다가 다시 올라오는 포물선의 특성 때문에
이차함수는 $x$축을 지나지 않을 때도 있습니다.

이차함수의 $x$절편은
$2$개거나 $1$개거나 없을 수도 있죠.
자 그럼 절편은 어떻게 구할까요?
$y$축과 만났다는 건, $x=0$ 이라는 뜻이고,
$x$축과 만났다는 건, $y=0$ 이라는 뜻이죠.
따라서, 주어진 식에 $x=0$ 과 $y=0$ 을 대입하면 됩니다.
이 경우엔 표준형보다는
전부 전개가 되어있는 편이 계산이 쉽습니다.
예를 들면, $y=(x-2)^2-1$ 보다는
$y=x^2-4x+3$ 가 절편을 구하기엔 좋다는 거죠.
이를 일반형이라고 합니다.
이때, $y$절편은 $x=0$ 을 대입해서,
$3$이 됩니다.
$x$절편은 $y=0$ 을 대입해서,
$x^2-4x+3=(x-1)(x-3)=0$ 이므로,
$x=1$ 또는 $x=3$ 이 되죠.
■ 이차함수의 그래프의 절편
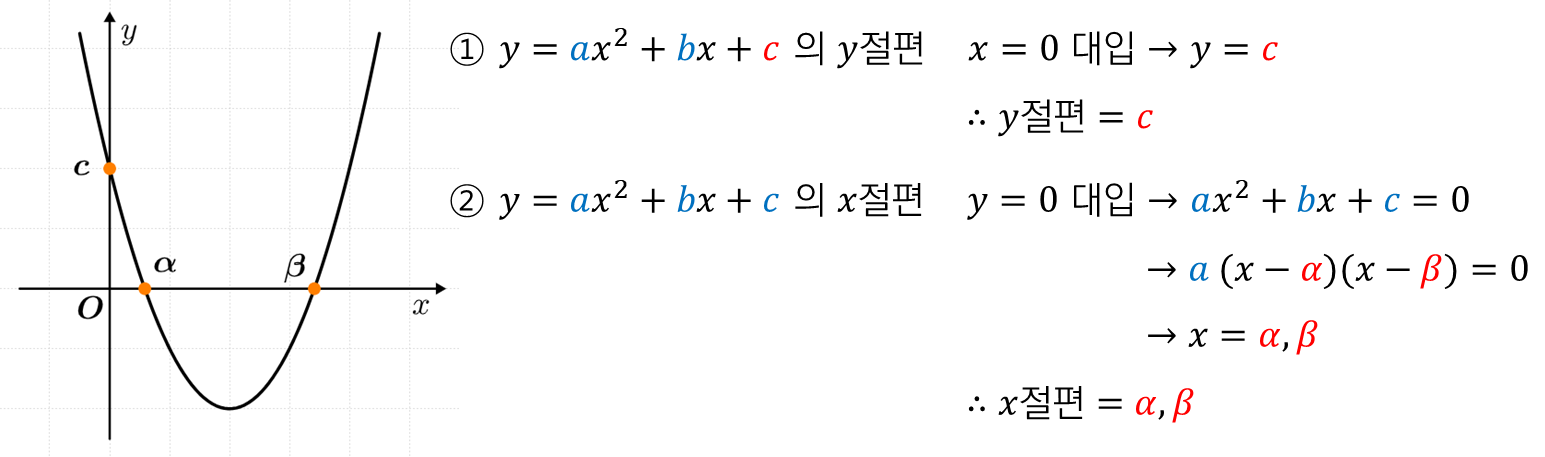
마무리
여기까지!
이차함수의 두 종류 점을 알아봤습니다.
보통은 꼭짓점과 $y$절편만 찍으면
이차함수 그래프를 그릴 수 있죠.
다음엔 그래프의 성질에 대해 알아볼게요!
'공통수학1 [고1] > 6. 이차함수' 카테고리의 다른 글
| 이차함수 그래프와 직선의 위치관계 (0) | 2023.10.22 |
|---|---|
| 이차방정식과 이차함수의 관계 (0) | 2023.10.13 |
| 이차함수의 일반형 (0) | 2023.09.10 |
| 이차함수의 그래프의 성질 (0) | 2023.09.07 |
| 이차함수의 표준형 (0) | 2023.08.29 |





댓글