이차함수의 표준형

■ 목표

- 이차함수의 표준형 유도하기

 

 

 

 

 

개요

 

중3-2 과정에서 이미

이차함수의 기본에 대해선 전부 배웠을 겁니다.

하지만, 제대로 복습을 한번 하려고 해요.

 

 

고등수학에서는

이차함수의 그래프 자체가 하나의 훌륭한 도구로써

많은 문제 풀이에 활용되기 때문이죠.

 

 

수(상)에서는

이차방정식과 이차부등식의 문제 풀이에

이차함수 그래프를 활용합니다.

 

 

 

이차함수의 표준형

 

표준형이란, 이차함수의 식을

"그래프를 그리기 쉬운 식" 으로 바꾼 형태를 말합니다.

다음과 같은 모양이죠.

 

 

$$y=a(x-p)^2+q$$

 

 

여기서  $a$,  $p$,  $q$ 의 의미가 무엇인지,

또, 왜 그런지를 정확히 이해하는 것이 중요해요.

표준형의 유도과정은 다음과 같습니다.

 

 

■ 이차함수의 표준형 유도과정

먼저, 가장 기본적인 형태이죠.

"$x$ 에 제곱이 된다면,  $y$ 는 어떻게 변하는가" 입니다.

 

 

① 기본 이차함수 : $y=x^2$

여기서의 핵심은

$y$ 가 훨씬 빠르게 커지므로 그래프는 "곡선형태" 이고,

$x$ 가 "음수든, 양수든 같은 값" 이 나온다는 것입니다.

이 모양은 포물선이라고도 합니다.

 

---

 

② 방향과 폭 a의 변화 : $y=$$a$$x^2$

 

먼저,  $a$ 가 음수라면, 모든  $y$ 값이 음수가 되고,

그래프는  $x$ 축을 기준으로 아래로 뒤집혀 그려집니다.

이를 "위로 볼록하다" 라고 얘기하죠.

즉,  "$a$ 의 부호" 는 그래프의 방향을 결정합니다.

 

 

또,  "$a$ 의 절댓값의 크기" 가 커질수록

$y$ 는 더 빨리 변하므로, 그래프의 폭은 좁아집니다.

 

---

 

③ x축 평행이동 : $y=(x-$$p$$)^2$

 

많이들 헷갈려하는 부분이죠?

오른쪽으로  $+1$ 만큼 이동했다면, 식은  $y=(x-1)^2$ 이 됩니다.

$x=1$ 을 넣어야,  $y=0$ 이 되기 때문이죠.

 

---

 

④ y축 평행이동 : $y=x^2+$$q$

 

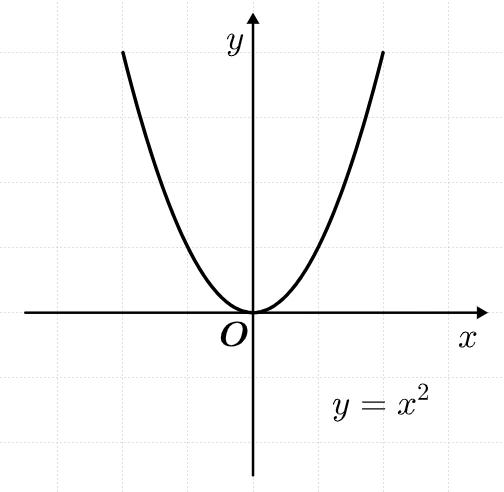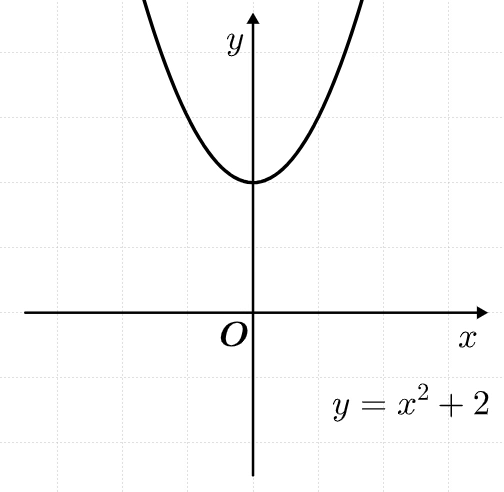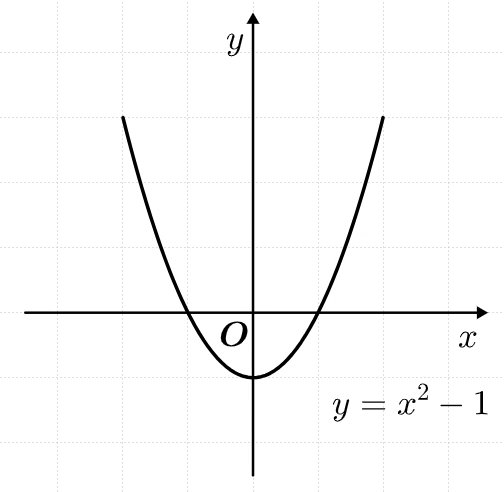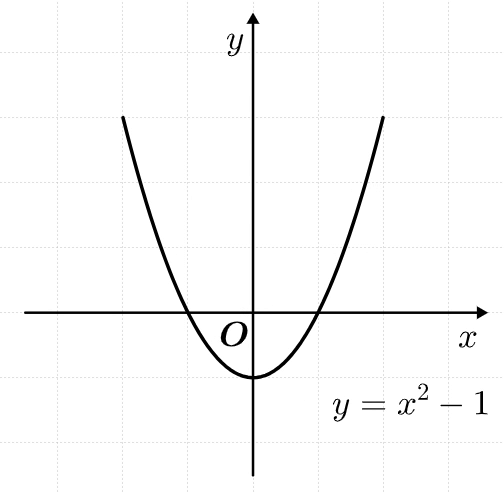
위아래로 이동하는  $y$축 평행이동은

말 그대로  $y$ 에 얼마를 더해주느냐로 표현됩니다.

 

---

 

이 모든 내용을 종합하면

이제 모든 이차함수의 그래프를 쉽게 그릴 수 있게 되죠.

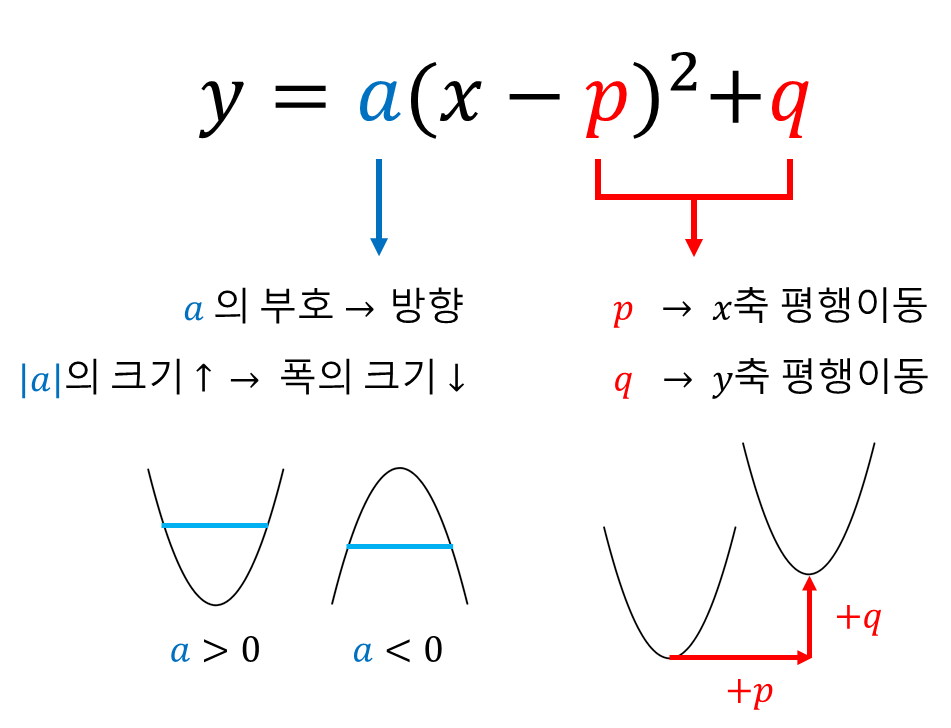
각 상수의 의미를 정리하면 다음과 같습니다.

 

 

■ 이차함수의 표준형

​

 

 

마무리

 

함수는  $x$ 와  $y$ 의 관계를 알아내는 것이고,

그 핵심도구는 그래프입니다.

 

이차함수도 표준형을 보고, 그래프 그리는 연습을 많이 하면

이차함수를 깊이 이해할 수 있을 거예요.

여기까지!