이차함수의 그래프의 성질

 

 

■ 목표

- 이차함수의 그래프의 증가와 감소 표현하기

- 이차함수의 그래프의 대칭성 이해하기

 

 

 

 

 

개요

 

함수란  "$x$와  $y$의 관계" 를 말합니다.

$x$가 변할 때,  "$y$는 어떻게 변하는지" 를

설명할 수 있어야 하죠.

 

 

그래서 그 변화를 한눈에 볼 수 있도록

그래프를 그리게 됩니다.

 

 

여기서는 이차함수의 그래프를 살펴보면서

그 특징들을 알아볼게요.

 

 

 

이차함수의 그래프의 증가와 감소

 

"$x$와  $y$의 관계" 를 표현하는 가장 단순한 방법은

바로  $y$값의 증가와 감소입니다.

 

 

$x$ 에 점점 큰 수를 넣었을 때,

$y$ 도 따라 커지는지, 반대로 작아지는 지를 표현하는 거죠.

 

 

이를 그래프에선 어떻게 알 수 있을까요?

---

 

 

먼저,  $x$ 축은 가로선입니다.

오른쪽으로 갈수록 커지고, 왼쪽으로 갈수록 작아지죠.

 

 

$y$ 축은 세로선입니다.

위로 갈수록 커지고, 아래로 갈수록 작아지죠.

 

 

함수의 그래프에서는

$x$ 가 오른쪽으로 움직일 때(증가),

$y$ 는 올라가는지(증가), 내려가는지(감소)를 보면 됩니다.

 

---

이차함수의 그래프는 다음과 같습니다.

 

 

 

 

$x$가 오른쪽으로 움직일 때,

$y$는 내려오다가(감소) 꼭짓점을 지난 후,

다시 올라가죠(증가).

 

 

그래서  $x$의 범위에 따라

$x<0$ 일 때는 감소

$x>0$ 일 때는 증가

이렇게 따로 표현하면 됩니다.

 

 

이때, 중요한 건 증가/감소가 바뀌는 기준점이고,

"꼭짓점의  $x$좌표" 가 그 기준이라는 점입니다.

 

 

 

이차함수의 그래프의 대칭성

 

이차함수의 가장 큰 특징은

말 그대로 이차식인  $x^2$ 때문에 생깁니다.

 

 

$x$ 가 양수든 음수든  "제곱" 이 되면,

$y$ 는 양수가 나오게 되죠.

 

 

그래프에서는

"같은  $y$값을 가진 점" 이 두 개씩,

어떤 선을 중심으로 좌우 대칭인 모양이 됩니다.

즉,  "선대칭 도형"이죠.

 

 

 

 

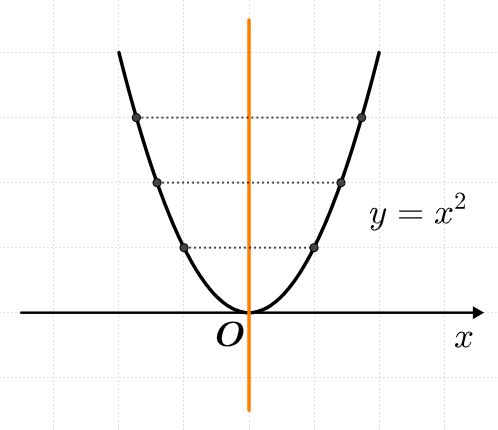
그래서 이차함수의 그래프의 성질은

한 단어로  "대칭성" 입니다.

그리고 그 기준선을  "(대칭)축" 이라고 부릅니다.

 

---

이제 축을 식으로 표현하는 방법입니다.

$y$축에 평행한 선은,  $x=p$ 라는 식으로 표현되죠.

"$x$ 값이 똑같은 모든 점을 이은 선" 이라는 뜻입니다.

 

 

이 식은 함수는 아니기 때문에,

"축의 방정식" 이라고 부릅니다.

 

 

축의 방정식은 반드시 꼭짓점을 지나기 때문에,

"꼭짓점의  $x$좌표" 와 같습니다.

그래서 표준형의 이차함수식에서는

축의 방정식을 바로 알 수 있죠.

 

 

■ 이차함수의 그래프의 대칭성

​

 

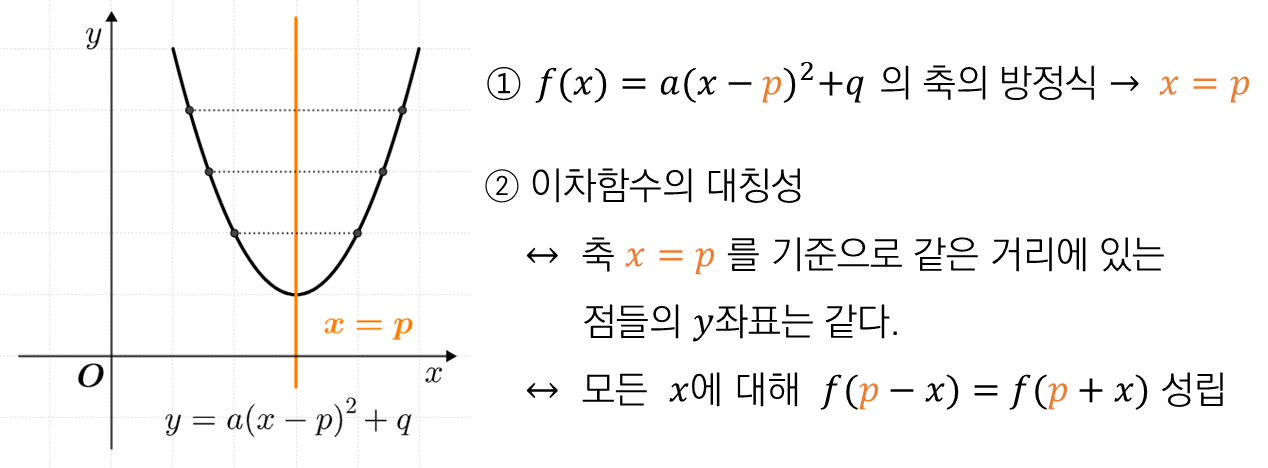
여기서 대칭성을 표현하는

마지막 문장이 중요합니다.

 

 

모든  $x$ 에 대해서라고 했으니,

$x=1$ 을 대입한  $f(p-1)=f(p+1)$ 도 성립하죠.

 

 

해석해 보면,

$x=p$ 를 기준으로  $1$ 만큼 왼쪽으로 가든, 오른쪽으로 가든

$y=f(x)$ 값은 같다는 뜻입니다.

즉,  축이  $x=p$ 라는 걸 알려주는 조건이 됩니다.

 

 

 

마무리

 

여기까지!

아주아주 중요한 이차함수의 그래프의 성질이었습니다.

 

하나의 그래프에 대해 자세히 알고 있으면,

그 성질을 암시하는 여러 조건을 보고도

쉽게 그래프를 그리거나 해석해 낼 수 있습니다.

심화문제에서 자주 요구하는 능력이죠.