■ 목표
- 방정식과 항등식의 의미 알기

등식의 분류 - 방정식과 항등식
"두 식의 관계" 를 기준으로 식을 분류해보면
등식과 부등식으로 나눌 수 있었죠.

이번엔 등식을 조금 더 살펴보려고 합니다.
등식은 말 그대로 등호(=) 를 중심으로
"왼쪽과 오른쪽이 같다" 는 뜻이죠.
다만, 어떤 두 식을 양 쪽에 놓느냐에 따라
의미와 해석이 완전히 달라집니다.
① 서로 다른 두 식인 경우

왼쪽은 ($x$ 에 대한 2차식), 오른쪽은 ($0$)
딱 봐도 양쪽의 식이 다른데, 등호가 있으니 같아야 합니다.
그래서 왼쪽이 식이 $0$ 이 되기 위해서는

$x$ 는 반드시 $2$ 또는 $3$ 이어야만 합니다.
이렇게 $x$ 가 "특정값일 때만 성립하는 등식" 을
방정식이라고 합니다.
그래서 방정식을 푼다는 것은
등식을 성립하게 하는
"특정 $x$ 값을 찾는다"는 뜻이죠.
② 완전히 동일한 두 식인 경우

??? 너무 당연한 말 아닌가요?
맞습니다.
하지만, 약간 형태를 바꿔주면

왠지 달라보이게도 할 수 있죠.
그래서 대충 보면 양 쪽의 식은 달라 보이지만,
왼쪽 식을 인수분해 혹은 오른쪽 식을 전개해보면
"완전히 동일한 식" 이라는 것을 알 수 있죠.
굳이 이 식을 만족하기 위한 $x$ 를 찾아보자면
당연히 무수히 많습니다.
이렇게 "모든 $x$ 에 대해 항상 성립하는 등식"을
항등식이라고 합니다.
이 당연한 식은 생각보다 활용도가 높습니다.
■ 정리
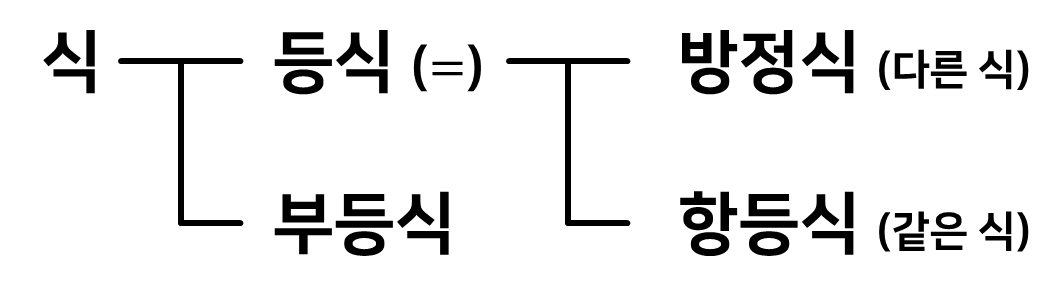
이처럼 등식은 두가지로 나뉘는데, 두 식에서의 목적은 다릅니다.
방정식은 두 식을 같게 하는 "특정값을 찾는 것" 이 목적이고,
항등식은 항상 "두 식이 동일하다는 것을 이용" 하는 것이 목적이죠.
마무리
여기까지!
다음은 이 당연해보이는 항등식을 어떻게 이용할지
어떻게 문제들을 풀어낼지부터 차근차근 시작해보려 합니다.
'공통수학1 [고1] > 2. 항등식과 나머지정리' 카테고리의 다른 글
| 나머지정리1 [1차식/2차식으로 나눈 나머지] (0) | 2022.11.07 |
|---|---|
| 나눗셈에 대한 항등식 (0) | 2022.11.06 |
| 항등식의 풀이 - B. 수치대입법 (0) | 2022.10.10 |
| 항등식의 풀이 - A. 계수비교법 (0) | 2022.10.09 |
| 식의 종류 (0) | 2022.10.06 |





댓글