■ 목표
- 공통부분이 있는 함수 분석하기
- 공통부분이 있는 함수의 최대/최소 구하기

개요
공통부분이라는 단어를 봤을 때,
여러분이 바로 떠올려야 하는 것은 바로 치환입니다.
치환은 길고 복잡해 보이는 식을 단순하게 만들어서,
문제를 이해하기 쉽게 도와주죠.
근데 함수에서의 치환은 좀 더 의미가 특별합니다.✨한번 차근차근 알아볼까요?
공통부분이 있는 함수
다음과 같은 함수가 있다고 해보죠.

식을 보자마자 바로 전개해서
$y=x^4-4x^3+8x^2-8x+2$ 라고 쓰더라도
아직 사차함수에 대해서는 아무것도 할 수가 없습니다.
그래서 전개하는 대신 한 눈에 보이는 공통부분인
$(x^2-2x)$ 에 집중을 하기로 합니다.🔍
$(x^2-2x)$ 를 새로운 문자인 $t$ 로 치환하면
새로운 시각으로 볼 수 있습니다.🕶️

원래 있었던 사차함수는 이제 이차함수처럼 보입니다.
하지만, 문자가 $x$ 가 아니라 $t$ 가 되었죠.
그래서 이젠 $x=1$ 일 때, $y$ 가 얼마인지 구할 때에도
한번 더 생각해야합니다.🤔
$x=1$ 이라면, $t=-1$ 인 것이고,
$t=-1$ 일 때, $y=-1$ 이 되는 것이죠.
여기서의 핵심은
$(x^2-2x)$ 를 단순히 $t$ 로 바꿔 썼다고 보는 것이 아니라,
$t=(x^2-2x)$ 를 하나의 함수로써 바라보는 것입니다.
원래는 $x$ 를 넣으면 바로 $y$ 가 나오는 함수였지만,
사차함수라서 너무 복잡했기 때문에,
치환을 이용해 두 개의 함수로 분리한 셈이죠.
'$x$ 를 넣으면 $t$ 가 나오는' 함수
'$t$ 를 넣으면 $y$ 가 나오는' 함수
이렇게요.

이 개념은 굉장히 중요합니다.⭐
나중에 수(하)에서 배울 합성함수에 대한 개념이기도 하죠.
공통부분이 있는 함수의 최대/최소
이제 공통부분이 있는 함수의 최대/최소를 구해보죠.
이때, 제한된 범위에서 최대/최소 구하는 방법에 대해 잘 알고 있어야 합니다.
<제한된 범위에서 이차함수의 최대/최소>
제한된 범위에서의 이차함수의 최대최소
■ 목표 - A. 범위 내에 꼭짓점이 있을 때, 최대/최소 구하기 - B. 범위 내에 꼭짓점이 없을 때, 최대/최소 구하기 개요 제목만 봐도 지난 포스팅에서 그대로 이어지는 내용이란 걸 알 수 있죠. 이차
indv-wrappedmath.tistory.com
예시를 통해 바로 살펴볼게요.
■ 예시

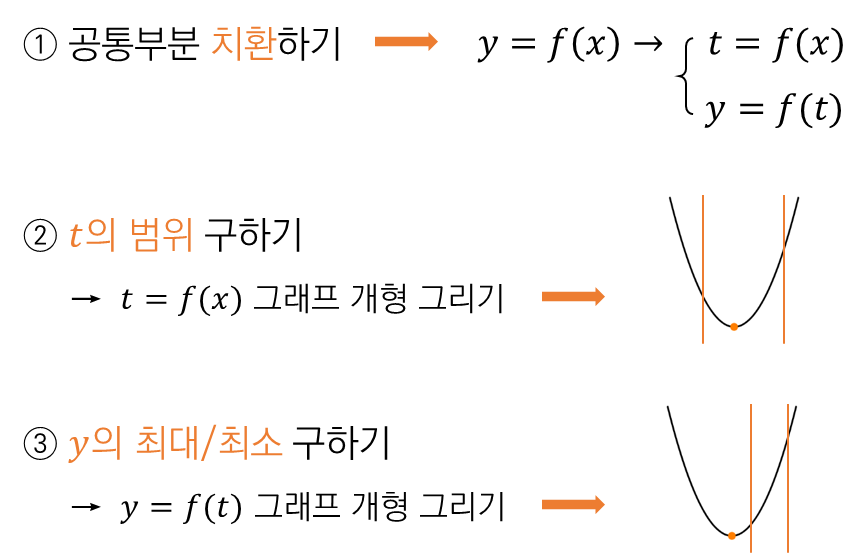
① 치환
$(x^2-2x)$ 를 $t$ 로 치환합니다.
이는 두 개의 함수로 분리했다는 뜻이기도 합니다.
$t=x^2-2x$ 와 $y=t^2+4t+2$ 로 말이죠.
② $t$ 의 범위 구하기
$y$ 의 최대/최소를 구하고 싶지만, $x$ 를 바로 대입할 순 없습니다.
그래서 $t=(x^2-2x)$ 를 살펴보고,
'$x$ 의 범위' 를 '$t$ 의 범위' 로 바꿔보려 합니다.
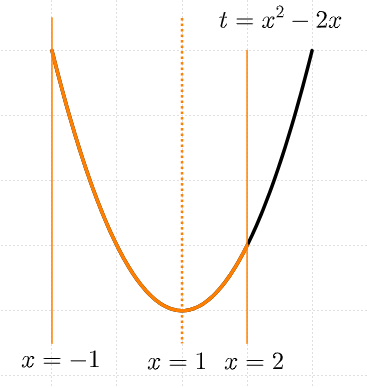
축과 범위를 표시해 보면
$x=1$ 일 때, 최솟값은 $t=-1$
$x=-1$ 일 때, 최댓값은 $t=3$
임을 알 수 있습니다.
즉, $-1 \leq t \leq 3$ 이 $t$의 범위가 됩니다.
③ $y$ 의 최대/최소 구하기
이제 문제는 이렇게 바뀌었다고 볼 수 있습니다.

마찬가지로, 그래프의 개형을 이용해 구해주면 됩니다.

$t=-1$ 일 때, 최솟값은 $y=-1$
$x=3$ 일 때, 최댓값은 $y=23$
■ 공통부분이 있는 함수의 최대/최소 구하기
마무리
많이들 어려워하는 유형이라고 볼 수 있죠.
하지만, 뜯어보면 결국은
제한된 범위에서 이차함수의 최대/최소를 두 번 구해야 하는 유형에 불과하기도 해요.
많이 연습해 보면 그만큼 쉬워진답니다
'공통수학1 [고1] > 6. 이차함수' 카테고리의 다른 글
| 이차함수의 최대최소[응용] - 2.이차식의 최대최소 (7) | 2023.12.03 |
|---|---|
| 제한된 범위에서의 이차함수의 최대최소 (2) | 2023.11.13 |
| 이차함수의 최대최소 (2) | 2023.11.04 |
| 이차함수 그래프와 직선의 위치관계 (0) | 2023.10.22 |
| 이차방정식과 이차함수의 관계 (0) | 2023.10.13 |





댓글