제한된 범위에서의 이차함수의 최대최소

■ 목표

- A. 범위 내에 꼭짓점이 있을 때, 최대/최소 구하기

- B. 범위 내에 꼭짓점이 없을 때, 최대/최소 구하기

 

 

 

 

 

개요

 

제목만 봐도 지난 포스팅에서 그대로 이어지는 내용이란 걸 알 수 있죠.

 

 

<이차함수의 최대최소>

이차함수의 최대최소

 

 

달라진 점은  "제한된 범위에서의"

즉,  $x$ 의 범위가 추가되었다는 뜻입니다.

 

 

 

제한된 범위에서 이차함수는 최대/최소를 둘 다 갖게 됩니다.

따라서, 단순히 꼭짓점을 구하는 것 외에도 범위를 생각해야만 하죠.🤔

 

 

범위가 어떻게 주어지느냐에 따라 다음과 두 가지로 나누어 생각해보려고 합니다.

A. 범위 내에 꼭짓점이 있을 때

B. 범위 내에 꼭짓점이 없을 때

 

 

 

A. 범위 내에 꼭짓점이 있을 때

 

범위 내에 꼭짓점이 있다면 꼭짓점이 최대나 최소가 된다는 건 분명합니다.

그렇다면 범위를 잘라내면서 나오는 나머지 최소나 최대를 구해주는 것이 문제겠죠.

 

---

■ 예시

 

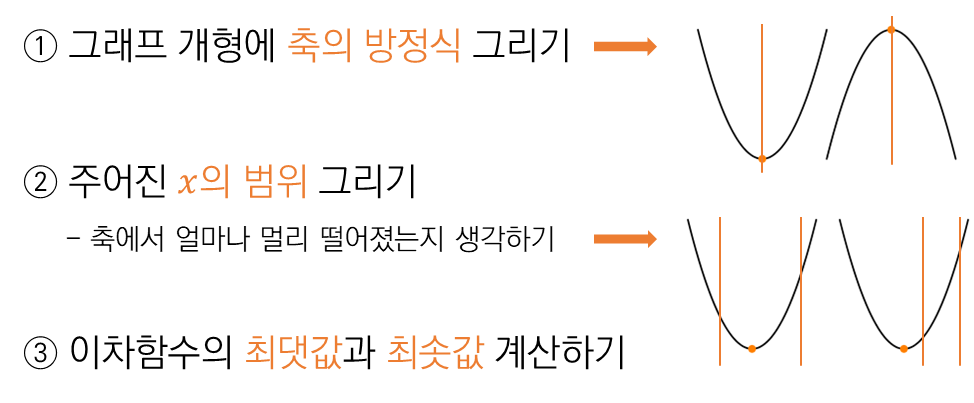
① 축의 방정식 찾기

$y=x^2-2x-3=(x-1)^2+□$ 이므로,

축의 방정식은  $x=1$ 임을 알 수 있죠.

 

 

 

② 주어진 범위 표시하기

범위의 시작인  $x=-1$ 과 끝인  $x=2$를 표시해 주면 됩니다.

하지만, 이 때 한 가지를 염두에 두고 그려주는 것이 좋습니다.

바로 이차함수의 대칭성입니다.⚖️

 

 

이차함수는 축을 중심으로 그래프가 좌우대칭이라는 거죠.

여기서는  $x=1$ 이 중심이기 때문에,

한 칸씩 멀어진  $x=0$ 과  $x=2$ 의 값이 같습니다.

 

 

 

따라서, 축으로부터 가장 멀리 떨어진

$x=-1$ 일 때가 최댓값임을 알 수 있죠.

 

 

③ 최솟값, 최댓값 구하기

$x=1$ 일 때, 최솟값은  $y=-4$

$x=-1$ 일 때, 최댓값은  $y=0$

 

 

 

B. 범위 내에 꼭짓점이 없을 때

 

범위 내에 꼭짓점이 없다면 확실한 최대/최소는 없습니다.

따라서, 범위 안에서 최대/최소를 둘 다 찾아줘야 하죠.😥

 

 

다행히도 꼭짓점 없는 범위에서 이차함수는

계속 증가하거나, 감소하기 때문에 쉽게 최대/최소를 찾을 수 있습니다.

 

---

■ 예시

 

① 축의 방정식 찾기

축의 방정식은  동일한  $x=1$ 입니다.

하지만, 방향은 반대죠.

 

 

 

② 주어진 범위 표시하기

범위인  $x=2$ 부터  $x=3$ 까지가 모두

축보다 오른쪽에 있다는 것이 중요합니다.

 

 

 

③ 최솟값, 최댓값 구하기

$x=2$ 일 때, 최댓값은  $y=3$

$x=3$ 일 때, 최솟값은  $y=0$

 

 

■ 제한된 범위에서의 이차함수의 최대최소 구하기

​

 

 

마무리

 

단순히 최대최소 문제에서 조건 하나만 추가한 것 같지만,

이차함수의 대칭성에 대해 잘 이해하고 있어야

효과적으로 풀 수 있는 좋은 유형이었죠?😃

 

다음엔 이 최대최소를 활용한 여러 가지 유형의 문제들을

풀어보도록 해요.